H_
Nilpotent Transformations
SKIP_
p1
QM_[0;true;false;true;false;true;true;true;false]
Let A and B be square n by n matrices.
-
AS_[true;false]
If A and B are similar matrices and A is nilpotent, then so is B.
-
AS_[true;false]
If A is nilpotent, then A has an inverse which is nilpotent.
-
AS_[true;false]
If A is nilpotent, then so is the transpose of A.
-
AS_[true;false]
If A has determinant zero, it is nilpotent.
-
AS_[true;false]
If A is nilpotent, then A has 0 as an eigenvalue.
-
AS_[true;false]
If A is nilpotent, then A has no eigenvalues except 0.
-
AS_[true;false]
If A is nilpotent, its index of nilpotency can be no larger than its
dimension n.
-
AS_[true;false]
If A is nilpotent, its index of nilpotency can be no larger than its
dimension n - 1.
SKIP_
p2
QM_[0;true;false;true;false;true;true]
Let A be an n by n upper triangular matrix.
AH_[2]
-
AS_[true;false]
Every entry on the diagonal of A is an eigenvalue of A.
-
AS_[true;false]
Every column vector with only one non-zero entry is an eigenvector of A.
-
AS_[true;false]
A is nilpotent if and only if all the diagonal entries of A are zero.
-
AS_[true;false]
If A is nilpotent, then
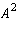 has the entry in the upper right hand corner
zero, i.e.
has the entry in the upper right hand corner
zero, i.e. 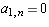 .
.
-
AS_[true;false]
If A is nilpotent, then
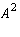 has all its elements directly above the
diagonal are zero. (i.e.
has all its elements directly above the
diagonal are zero. (i.e. 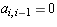 for i = 2, 3, ..., n.)
for i = 2, 3, ..., n.)
-
AS_[true;false]
If A is nilpotent and all the entries above the diagonal are positive, then
the index of nilpotency is exactly n.
SKIP_
p3
QM_[0;n;true;r;r;1]
Let A be an n by n matrix with entries on the superdiagonal non-zero
(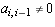 for i = 2, 3, ..., n.) and with all other entries zero.
AH_[2]
for i = 2, 3, ..., n.) and with all other entries zero.
AH_[2]
-
The index of nilpotency of A is exactly
AS_[1;2;n-1;n;n+1]
.
-
AS_[true;false]
Let B be any nilpotent square n by n matrix and v be a non-zero vector. The
vectors
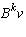 for k = 0, 1, 2, ... span a subspace W of
for k = 0, 1, 2, ... span a subspace W of 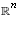 and
the linear map corresponding to B maps W into W.
and
the linear map corresponding to B maps W into W.
-
With B, v, and W as in the last part, let r be the smallest positive integer
with
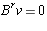 . Then the index of nilpotency of the linear map of W
corresponding to B is exactly
AS_[1;2;r-1;r;r+1;n-1;n;n+1]
.
. Then the index of nilpotency of the linear map of W
corresponding to B is exactly
AS_[1;2;r-1;r;r+1;n-1;n;n+1]
.
-
With B, v, and W as in the last part, the dimension of W is precisely
AS_[1;2;r-1;r;r+1;n-1;n;n+1]
.
-
With B, v, and W as in the last part, the matrix of the linear map from
W to W corresponding to B is a matrix with subdiagonal elements all equal to
AS_[0;1;2;r-1;r;r+1;n-1;n;n+1]
(with respect to the basis of the
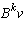 's).
's).
SKIP_
p4
QM_[0;3;2;3;1;0;4;5]
Let T be a linear map which maps 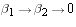 and
and 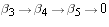 where the
where the
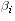 are a basis of
are a basis of 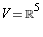 .
AH_[2]
.
AH_[2]
-
The index of nilpotency of T is
AS_[0;1;2;3;4;5]
.
-
The dimension of the nullspace of T is
AS_[0;1;2;3;4;5]
.
-
The dimension of the image space TV is
AS_[0;1;2;3;4;5]
.
-
The dimension of the space
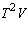 is
AS_[0;1;2;3;4;5]
.
is
AS_[0;1;2;3;4;5]
.
-
The dimension of the space
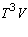 is
AS_[0;1;2;3;4;5]
.
is
AS_[0;1;2;3;4;5]
.
-
The nullity of
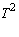 is
AS_[0;1;2;3;4;5]
and the nullity of
is
AS_[0;1;2;3;4;5]
and the nullity of 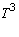 is
AS_[0;1;2;3;4;5]
.
is
AS_[0;1;2;3;4;5]
.
SKIP_
p5
QM_[0;4;5;3;1;0;2;4;6;7;e7;e5;e3;e1;e6;e4;e2]
Let A be the 7 by 7 matrix with all entries 0 except that the diagonal
above the superdiagonal is filled with entries equal to 1. Let V denote
the vector space 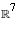 .
AH_[2]
.
AH_[2]
-
The matrix A has index of nilpotency
AS_[0;1;2;3;4;5;6;7]
.
-
The dimensions of
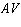 ,
, 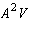 ,
, 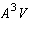 , and
, and 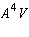 are
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
, and
AS_[0;1;2;3;4;5;6;7]
respectively.
are
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
, and
AS_[0;1;2;3;4;5;6;7]
respectively.
-
The nullities of
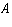 ,
, 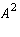 ,
, 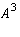 , and
, and 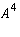 are
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
, and
AS_[0;1;2;3;4;5;6;7]
respectively.
are
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
, and
AS_[0;1;2;3;4;5;6;7]
respectively.
- If e1, e2, ..., e7 are the standard basis of
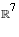 , then
the linear map represented by A can be expressed as
AS_[e1;e2;e3;e4;e5;e6;e7]
, then
the linear map represented by A can be expressed as
AS_[e1;e2;e3;e4;e5;e6;e7]
 AS_[e1;e2;e3;e4;e5;e6;e7]
AS_[e1;e2;e3;e4;e5;e6;e7]
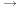 AS_[e1;e2;e3;e4;e5;e6;e7]
AS_[e1;e2;e3;e4;e5;e6;e7]
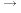 AS_[e1;e2;e3;e4;e5;e6;e7]
AS_[e1;e2;e3;e4;e5;e6;e7]
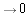 and
AS_[e1;e2;e3;e4;e5;e6;e7]
and
AS_[e1;e2;e3;e4;e5;e6;e7]
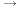 AS_[e1;e2;e3;e4;e5;e6;e7]
AS_[e1;e2;e3;e4;e5;e6;e7]
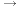 AS_[e1;e2;e3;e4;e5;e6;e7]
AS_[e1;e2;e3;e4;e5;e6;e7]
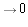 .
.
SKIP_
p6
QM_[0;2;0;1;0;0]
The A be the matrix
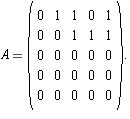
AH_[2]
When put in canonical form, the matrix is seen to have
AS_[0;1;2;3;4;5;6;7]
strings with 1 basis element,
AS_[0;1;2;3;4;5;6;7]
strings with 2 basis elements,
AS_[0;1;2;3;4;5;6;7]
strings with 3 basis elements,
AS_[0;1;2;3;4;5;6;7]
strings with 4 basis elements, and
AS_[0;1;2;3;4;5;6;7]
strings with 5 basis elements.
SKIP_
p7
QM_[0;true;true]
Let A be a square 2 by 2 nilpotent matrix.
AH_[2]
-
AS_[true;false]
If the index of nilpotency is 1, then A is the zero matrix.
-
AS_[true;false]
If the index of nilpotency is 2, then A has a string with two basis elements
(i.e. one of the form
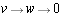 ).
).
SKIP_
p8
QM_[0;true;2;3]
Let A be a square 3 by 3 nilpotent matrix.
AH_[2]
-
AS_[true;false]
If the index of nilpotency is 1, then A is the zero matrix.
-
If the index of nilpotency is 2, then A can be represented with
a basis in which there is a string with one basis element and another
string with
AS_[0;1;2;3]
basis elements.
- If the index of nilpotency is 3, then A can be respresented with
a basis in which there is a single string with
AS_{0;1;2;3]
basis elements.
SKIP_
p9
QM_[0;true;false;false;true]
Let A be a square 4 by 4 nilpotent matrix.
AH_[2]
-
AS_[true;false]
If the index of nilpotency is 1, then A is the zero matrix.
-
AS_[true;false]
If the index of nilpotency is 2, then A can be represented with
a basis in which there are two strings with two basis elements each.
-
AS_[true;false]
If the index of nilpotency is 3, then A can be represented with
a basis in which there are two strings with one basis element and
another with two basis elements.
-
AS_[true;false]
If the index of nilpotency is 4, then A can be represented with
a basis in which there is a single string with 4 basis elements.
SKIP_
p10
QM_[0;true;true;true;true]
Let A be a square matrix. The characteristic polynomial of A
is the polynomial p(X) = det(A - Ix) where I is the n by n identity matrix.
-
AS_[true;false]
If B is similar to A, then A and B have the same characteristic polynomials.
-
AS_[true;false]
If B is similar to A and p, q are the characteristic polynomials of A and B
respectively, then p(A) = 0 if and only if q(B) = 0.
-
AS_[true;false]
If A is nilpotent and p is the characteristic polynomial of A, then p(A) = 0.
-
AS_[true;false]
If A is upper triangular with all its diagonal elements equal, then
p(A) = 0 where p is the characteristic polynomial of A.
SKIP_
p11
QM_[0;true]
AH_[2]
AS_[true;false]
If A is diagonalizable, then p(A) = 0 where p is the characteristic polynomial
of A.
SKIP_
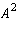 has the entry in the upper right hand corner
zero, i.e.
has the entry in the upper right hand corner
zero, i.e. 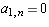 .
.
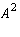 has all its elements directly above the
diagonal are zero. (i.e.
has all its elements directly above the
diagonal are zero. (i.e. 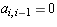 for i = 2, 3, ..., n.)
for i = 2, 3, ..., n.)
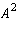 has the entry in the upper right hand corner
zero, i.e.
has the entry in the upper right hand corner
zero, i.e. 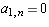 .
.
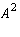 has all its elements directly above the
diagonal are zero. (i.e.
has all its elements directly above the
diagonal are zero. (i.e. 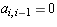 for i = 2, 3, ..., n.)
for i = 2, 3, ..., n.)
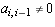 for i = 2, 3, ..., n.) and with all other entries zero.
AH_[2]
for i = 2, 3, ..., n.) and with all other entries zero.
AH_[2]
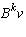 for k = 0, 1, 2, ... span a subspace W of
for k = 0, 1, 2, ... span a subspace W of 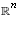 and
the linear map corresponding to B maps W into W.
and
the linear map corresponding to B maps W into W.
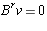 . Then the index of nilpotency of the linear map of W
corresponding to B is exactly
AS_[1;2;r-1;r;r+1;n-1;n;n+1]
.
. Then the index of nilpotency of the linear map of W
corresponding to B is exactly
AS_[1;2;r-1;r;r+1;n-1;n;n+1]
.
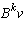 's).
's).
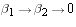 and
and 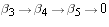 where the
where the
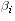 are a basis of
are a basis of 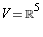 .
AH_[2]
.
AH_[2]
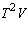 is
AS_[0;1;2;3;4;5]
.
is
AS_[0;1;2;3;4;5]
.
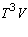 is
AS_[0;1;2;3;4;5]
.
is
AS_[0;1;2;3;4;5]
.
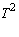 is
AS_[0;1;2;3;4;5]
and the nullity of
is
AS_[0;1;2;3;4;5]
and the nullity of 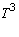 is
AS_[0;1;2;3;4;5]
.
is
AS_[0;1;2;3;4;5]
.
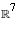 .
AH_[2]
.
AH_[2]
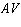 ,
, 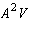 ,
, 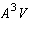 , and
, and 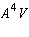 are
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
, and
AS_[0;1;2;3;4;5;6;7]
respectively.
are
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
, and
AS_[0;1;2;3;4;5;6;7]
respectively.
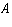 ,
, 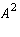 ,
, 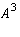 , and
, and 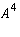 are
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
, and
AS_[0;1;2;3;4;5;6;7]
respectively.
are
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
,
AS_[0;1;2;3;4;5;6;7]
, and
AS_[0;1;2;3;4;5;6;7]
respectively.
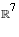 , then
the linear map represented by A can be expressed as
AS_[e1;e2;e3;e4;e5;e6;e7]
, then
the linear map represented by A can be expressed as
AS_[e1;e2;e3;e4;e5;e6;e7]
 AS_[e1;e2;e3;e4;e5;e6;e7]
AS_[e1;e2;e3;e4;e5;e6;e7]
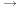 AS_[e1;e2;e3;e4;e5;e6;e7]
AS_[e1;e2;e3;e4;e5;e6;e7]
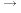 AS_[e1;e2;e3;e4;e5;e6;e7]
AS_[e1;e2;e3;e4;e5;e6;e7]
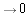 and
AS_[e1;e2;e3;e4;e5;e6;e7]
and
AS_[e1;e2;e3;e4;e5;e6;e7]
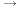 AS_[e1;e2;e3;e4;e5;e6;e7]
AS_[e1;e2;e3;e4;e5;e6;e7]
 AS_[e1;e2;e3;e4;e5;e6;e7]
AS_[e1;e2;e3;e4;e5;e6;e7]
 .
.
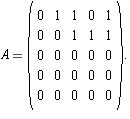
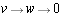 ).
).