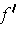 for the following:
for the following:
-
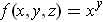
We have
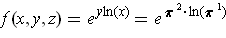 and so
by the chain rule, one has:
and so
by the chain rule, one has:
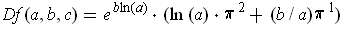 , i.e.
, i.e.
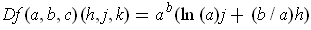 .
.
-
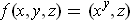
Using Theorem 2-3 (3) and part (a), one has:
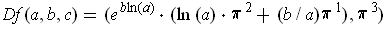 .
.
-
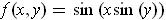 .
.
One has
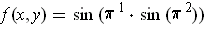 , and so by the chain rule:
, and so by the chain rule:
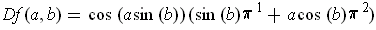
-
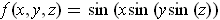
If
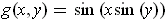 is the function of part (c), then
is the function of part (c), then
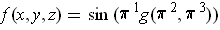 . Using the chain rule, we get:
. Using the chain rule, we get:
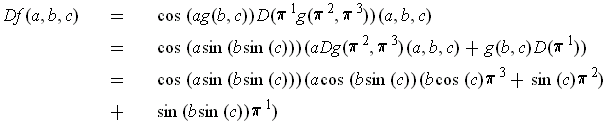
-
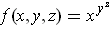
If
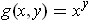 , then
, then
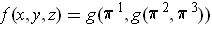 and
we know the derivative of
and
we know the derivative of
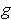 from part (a). The chain rule gives:
from part (a). The chain rule gives:
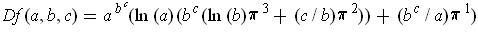
-

If
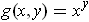 , then
, then
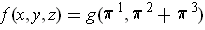 . So one gets:
. So one gets:
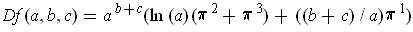 .
.
-
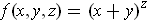
If
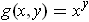 , then
, then
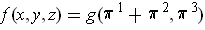 . So one gets:
. So one gets:
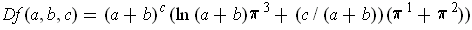 .
.
-
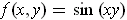
The chain rule gives:
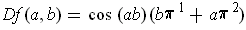 .
.
-
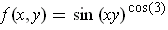
Using the last part:
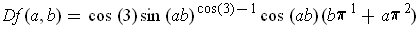 .
.
-
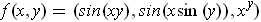
Using parts (h), (c), and (a), one gets
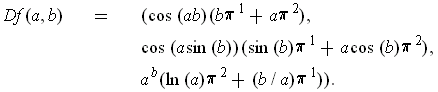
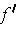 for the following (where
for the following (where
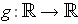 is continuous):
is continuous):
-
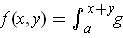 .
.
If
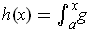 , then
, then
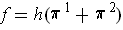 , and so:
, and so:
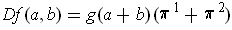 .
.
-
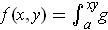 .
.
If
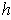 is as in part (a), then
is as in part (a), then
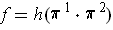 , and so:
, and so:
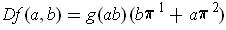 .
.
-
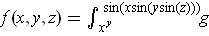 .
.
One has
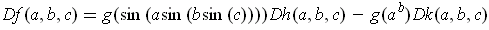 where
where
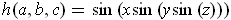 and
and
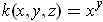 have
derivatives as given in parts (d) and (a) above.
have
derivatives as given in parts (d) and (a) above.
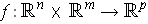 is bilinear if for
is bilinear if for
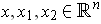 ,
,
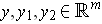 ,
and
,
and
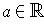 , we have
, we have
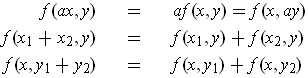
- Prove that if
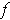 is bilinear, then
is bilinear, then
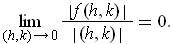
Let
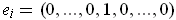 have a 1 in the
have a 1 in the
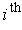 place only.
Then we have
place only.
Then we have
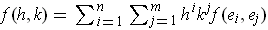 by
an obvious induction using bilinearity. It follows that there is an
by
an obvious induction using bilinearity. It follows that there is an
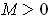 depending only on
depending only on
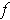 such that:
such that:
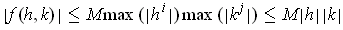 . Since
. Since
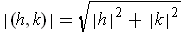 , we see that it
suffices to show the result in the case where
, we see that it
suffices to show the result in the case where
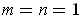 and the bilinear
function is the product function. But, in this case, it was verified in
the proof of Theorem 2-3 (5).
and the bilinear
function is the product function. But, in this case, it was verified in
the proof of Theorem 2-3 (5).
- Prove that
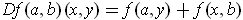 .
.
One has
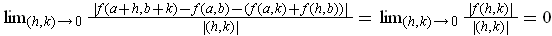 by bilinearity and part (a).
by bilinearity and part (a).
- Show that the formula for
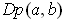 in Theorem 2-3 is a special case
of (b).
in Theorem 2-3 is a special case
of (b).
This follows by applying (b) to the bilinear function
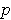 .
.
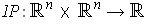 by
by
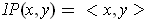 .
.
- Find
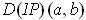 and
and
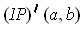 .
.
By Problem 2-12 and the fact that
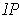 is bilinear, one has
is bilinear, one has
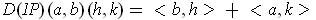 . So
. So
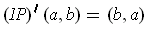 .
.
- If
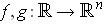 are differentiable, and
are differentiable, and
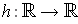 is defined by
is defined by
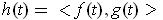 , show that
, show that
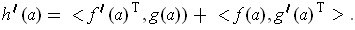
(Note that
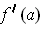 is an
is an
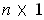 matrix; its transpose
matrix; its transpose
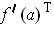 is an
is an
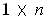 matrix, which we consider as a member of
matrix, which we consider as a member of
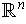 .)
.)
Since
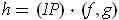 , one can apply the chain rule to get the
assertion.
, one can apply the chain rule to get the
assertion.
- If
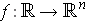 is differentiable and
is differentiable and
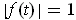 for all
for all
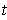 , show
that
, show
that
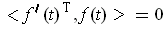 .
.
Use part (b) applied to
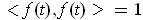 to get
to get
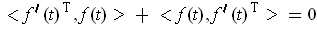 . This shows the result.
. This shows the result.
- Exhibit a differentiable function
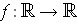 such
that the function |f| defined by |f|(t) = |f(t)| is not differentiable.
such
that the function |f| defined by |f|(t) = |f(t)| is not differentiable.
Trivially, one could let
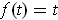 . Then
. Then
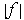 is not differentiable at 0.
is not differentiable at 0.
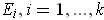 be Euclidean spaces of various dimensions.
A function
be Euclidean spaces of various dimensions.
A function
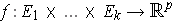 is called
multilinear if for each choice of
is called
multilinear if for each choice of
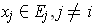 the function
the function
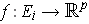 defined by
defined by
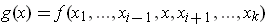 is a linear transformation.
is a linear transformation.
- If
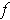 is multilinear and
is multilinear and
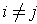 , show that for
, show that for
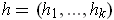 , with
, with
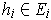 , we have
, we have
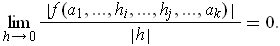
This is an immediate consequence of Problem 2-12 (b).
- Prove that
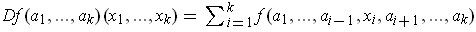 .
.
This can be argued similarly to Problem 2-12. Just apply the definition expanding the numerator out using multilinearity; the remainder looks like a sum of terms as in part (a) except that there may be more than two
 type
arguments. These can be expanded out as in the proof of the bilinear case to
get a sum of terms that look like constant multiples of
type
arguments. These can be expanded out as in the proof of the bilinear case to
get a sum of terms that look like constant multiples of
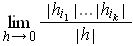
where
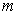 is at least two and the
is at least two and the
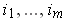 are distinct. Just as
in the bilinear case, this limit is zero. This shows the result.
are distinct. Just as
in the bilinear case, this limit is zero. This shows the result.
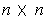 matrix as a point in the
matrix as a point in the
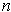 -fold product
-fold product
 by considering each row as a member of
by considering each row as a member of
 .
.
- Prove that
 is differentiable and
is differentiable and
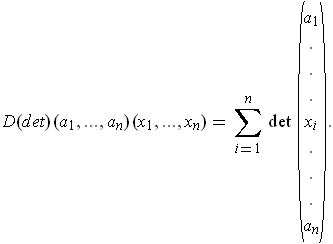
This is an immediate consequence of Problem 2-14 (b) and the multilinearity of the determinant function.
- If
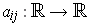 are differentiable and
are differentiable and
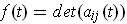 , show that
, show that
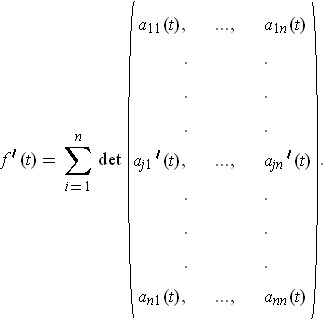
This follows by the chain rule and part (a).
- If
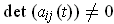 for all
for all
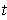 and
and
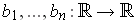 are differentiable, let
are differentiable, let
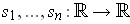 be the functions such that
be the functions such that
 are
the solutions of the equations:
are
the solutions of the equations:
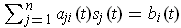 for
for
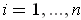 . Show that
. Show that
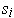 is differentiable and find
is differentiable and find
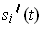 .
.
Without writing all the details, recall that Cramer's Rule allows you to write down explicit formulas for the
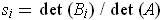 where
where
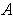 is the matrix of the coefficients
is the matrix of the coefficients
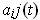 and the
and the
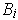 are obtained
from
are obtained
from
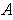 by replacing the
by replacing the
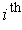 column with the column of the
column with the column of the
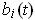 .
We can take transposes since the determinant of the transpose is the same
as the determinant of the original matrix; this makes the formulas simpler
because the formula for derivative of a determinant involved rows and so
now you are replacing the
.
We can take transposes since the determinant of the transpose is the same
as the determinant of the original matrix; this makes the formulas simpler
because the formula for derivative of a determinant involved rows and so
now you are replacing the
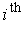 row rather than the
row rather than the
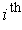 column.
Anyway, one can use the quotient formula and part (b) to give a formula
for the derivative of the
column.
Anyway, one can use the quotient formula and part (b) to give a formula
for the derivative of the
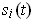 .
.
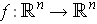 is differentiable and
has a differentiable inverse
is differentiable and
has a differentiable inverse
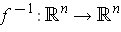 . Show
that
. Show
that
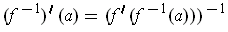 .
.
This follows immediately by the chain rule applied to
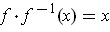 .
.