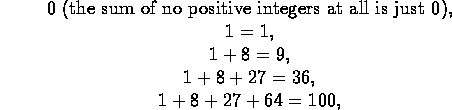
The method of finite differences can sometimes be used to guess a formula f(n) (but not to prove it). The way I am about to describe it requires that the values of f(n) be given for integer values of n beginning with n=0 (rather than 1). Let's use the example of guessing the formula for the sum of the cubes of the first n positive integers. We calculate a few values:
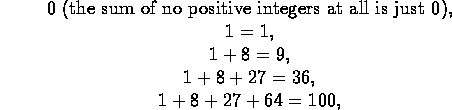
and then arrange them in a row. Then we build a difference table beneath them by subtraction:

We continue generating rows by this process until it appears that we get a row of 0's. This does not always happen, but when it does, we can build a polynomial formula for f(n). Using the first entries in each row, multiply the first entry of the first row by 1/0!, the first entry of the second row by n/1!, the first entry of the third row by n(n-1)/2!, the first entry of the fourth row by n(n-1)(n-2)/3!, the first entry of the fifth row by n(n-1)(n-2)(n-3)/4!, etc., and then add the results. (Remember that 0! is defined to be 1.) In our example, we get
![]()
which simplifies (you try it!) to
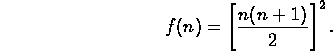
At this point we have not proved that this formula is correct, but at least we have a good guess for the formula, and we can try to prove it, e.g., by induction.