- Prove the formula for the sum of the first n natural numbers:

- Guess and prove a formula for the sum of the first n odd
natural numbers.
- Prove the formula for the sum of the first n+1 terms of an
arithmetic progression:
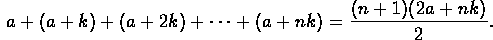
(Note that this equals the average of the first and last
terms, multiplied by the number of terms.)
- Prove the formula for the sum of the first n+1 terms of a
geometric progression:
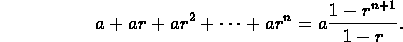
- Prove the formula for the sum of the squares of the first n
natural numbers:
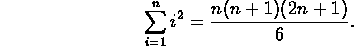
- Prove the formula for the sum of the cubes of the first n
natural numbers:
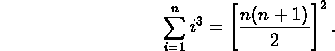
- The Fibonacci numbers are defined by
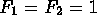 and thereafter
and thereafter
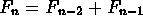 ,
, 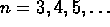 . Prove the formula:
. Prove the formula:
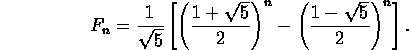
- Prove that the set
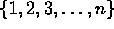 has exactly
has exactly 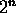 subsets.
subsets. - For nonnegative integers n and k, define
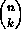 to be
the number of subsets of size k contained in a set of size n.
First prove (but not necessarily by induction!) that
to be
the number of subsets of size k contained in a set of size n.
First prove (but not necessarily by induction!) that
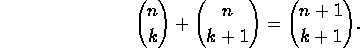
Then prove that
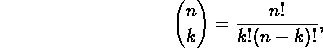
remembering that we define 0!=1.
- Prove the binomial formula:
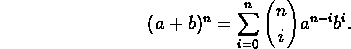
- Find and prove a formula for the number of ways n different men
can be completely paired up with n different women.
- A group of 2n individuals are to be paired off into n pairs
to play checkers. Find and prove a formula for the number of ways to
do this.
- Prove that the Tower of Hanoi puzzle with n disks can be
solved in
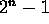 moves.
moves. - Find and prove a formula for the maximum number of regions a plane
can be divided up into using exactly n lines.
- Find and prove a formula for the maximum number of regions space
can be divided up into using exactly n planes.
- Observe that
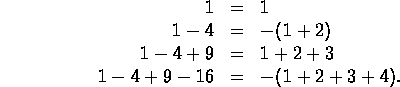
Guess and prove the general result.
- Guess and prove a formula for
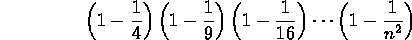
for 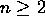 .
.
- Prove that every natural number greater than 1 can be factored
into powers of primes.
- Define (a,b) to be the
greatest common divisor of natural numbers a and b. Assume without
loss of generality that
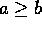 . Suppose c is the remainder when
a is divided by b.
. Suppose c is the remainder when
a is divided by b.
- Prove (without induction) that (b,c)=(a,b).
- Prove by induction (on what?)
that if z=(a,b) then there exist integers m and n
such that z=ma+nb.
- Prove (without induction) that if z is relatively
prime to m and z is a divisor mn, then z is a divisor of n.
- Let n be a natural number greater than 1. Assume that
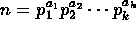 where
where 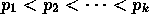 are
primes and
are
primes and 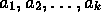 are positive natural numbers. Assume
also that
are positive natural numbers. Assume
also that
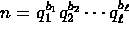 where
where
 are
primes and
are
primes and 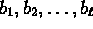 are positive natural numbers. Prove
by induction on n
that
are positive natural numbers. Prove
by induction on n
that 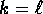 ,
, 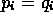 ,
, 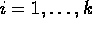 , and
, and 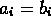 ,
,
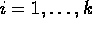 .
.
- Prove that the number of ways to divide up a convex n-gon,
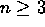 ,
into triangles using its diagonals is
,
into triangles using its diagonals is

- Three students, A, B, and C
are seated in a circle facing each other. There
is a supply of three red hats and two black hats, and the students are
aware of the types of hats available. The students close
their eyes, and a hat is placed on each one's head. The unused
two hats are hidden. When they
open their eyes, each can see the hats of the other two, but cannot
see their own hat. Unknown to them, each has been given a red
hat. Each one is asked in turn, ``Do you know the color of
your hat?'' A answers truthfully, ``No.'' B does the same.
But C's answer is ``Yes, my hat is red.'' How did C know this?
Generalize to n students.
![]()
![]()
![]()
![]()
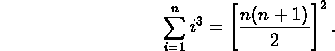
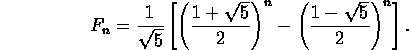
![]()
![]()
![]()
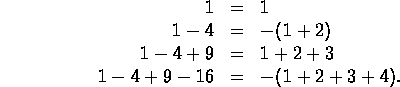
![]()
![]() .
.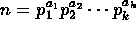 where
where 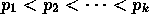 are
primes and
are
primes and 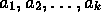 are positive natural numbers. Assume
also that
are positive natural numbers. Assume
also that
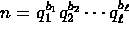 where
where
 are
primes and
are
primes and 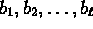 are positive natural numbers. Prove
by induction on n
that
are positive natural numbers. Prove
by induction on n
that 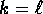 ,
, 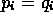 ,
, 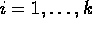 , and
, and 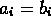 ,
,
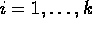 .
.
![]()