Chapter 2.3

Lecture 4 Chapter 2.3
Systems of Linear Equations Gauss Elimination.

• As we saw earlier, we think of systems of linear equations as augmented matrices, which means an array of the coefficients of all the variables together with the right hand sides. Thus the system
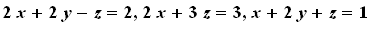   is converted to the matrix
• We next recall the concept of a pivot.  The pivot of a row is the first nonzero entry in it and the pivot position will be its column number. Sometimes, we may wish to mention both the row and column number for clarity.
  For a zero row (i.e. a row consisting of all zero entries) the pivot will be termed undefined  or missing  and its position will be said to be also undefined or  depending on our convenience. We say that the pivot positions for the above matrix are ( ).
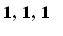• By row operations we shall learn to convert 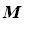 to the matrix  (row echelon form REF) first and then to the reduced row echelon form (RREF)   . We shall define these next.
• But first we observe that in the REF, we can read the equations from bottom to top and these can be easily solved by back substitution, giving values of 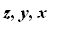    in order. In the last RREF case, we can simply read off the equations as giving the values of the variables. Thus the values are simply the entries in the last column! Naturally, REF is desirable and RREF is ideal for solving equations. We define these next.
• Definition of REF, RREF:  The REF occurs if we have a strictly increasing pivot position sequence, where the zero rows, if any, occur at the bottom of the matrix. RREF happens if we have REF and further each pivot is 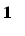 and is the only nonzero entry in its column.
• Here are some examples of REF, RREF or lack of these forms (Ans: No, REF,RREF,RREF).
           

Techniques of solution: Elementary operations:   

• We allow the following operations on a matrix, which correspond to standard manipulation of equations.
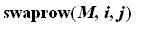•  which swaps the i-th and j-th rows of M, 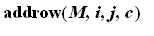 which adds c times the i-th row to the j-th row and mulrow(M,i,c) which replaces the i-the row by a nonzero c times itself.
• The plan is this. Among the pivot positions, bring the row with the smallest pivot position to the top and use addrow operations to kill entries below its pivot. Now fix this row and then repeat the process with the next rows. That means bring the row (from the next rows) with the smallest pivot position to the top and choose its pivot to make the lower rows have bigger pivot positions.
• Thus starting with our 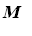, we have the following sequence. Here the pivot position sequences are:
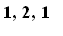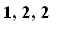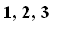  ( ), ( ), ( ) and we are done!
•     
  This is REF! To get RREF we do:
•        
• The final form is reached by dividing the three rows by their pivots to get:
   
• Figure out the operations! For example, the very first is
• The plan of these operations is this: Consider the pivot columns (columns with pivots in them). Start with the pivot in the last such column and using it clean the rest of the entries (there won't be any entries to clean below the pivot anyway).  Then continue with the earlier pivots in sequence.
  Finally change all pivots to 1 by dividing the corresponding rows by the pivots.
• The number of pivots used does not depend on who does the calculation, it is a property of the matrix called its RANK.  Of course, this statement is not obvious and needs proof.  Note that this is a property of the equation system, so the rank should not change if we choose different order of variables or make valid variable substitutions or make valid operations on the system. Thus it is a much deeper result than apparent! More on this later...
• The variables corresponding to the pivot columns are the pivot variables.   Their choice is not unique and indeed later we need to consider different such choices and choose the best among them.
• Solution of the system consists of expressing the pivot variables in terms of the non pivot variables, which are called free and can indeed be given arbitrary values!
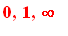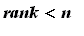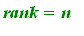• This gives the famous  rule. If there is a pivot in the last (augmented column)   then  we get an equation equating a zero with a nonzero number and there is no solution!  If this does not happen and if the pivot variables are fewer than the total number of varaibles (  = number of variables) , then there are free variables and hence infinitely many  solutions. Otherwise, if  then there is a unique solution! Practice checking these cases.
• All you need is an REF from the given system, so don't do RREF unless necessary . REF tells you if there are bad rows indicating no solution (pivot in the last column) and the rank; if this does not happen. Compare the rank with n for the conclusion!

>