Case of

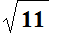
Now try another, namely

>	A:=matrix(2,4,[1,0,1,0,0,1,0,-11]);tvals:=[];

>	fun(A)(1,1);

>	seq([t,fun(A)(t,1)],t=1..5);

>	tvals:=[op(tvals),3];

>	A1:=ch(A,3,1);

>	fun(A1)(1,1);

>	seq([t,fun(A1)(1,t)],t=1..5);

>	tvals:=[op(tvals),3];A2:=ch(A1,3,2);

>	fun(A2)(1,1);

>	seq([t,fun(A2)(t,1)],t=1..8);

>	tvals:=[op(tvals),6];A3:=ch(A2,6,1);

>	fun(A3)(1,1);

>	seq([t,fun(A3)(1,t)],t=1..8);

>	tvals:=[op(tvals),3];A4:=ch(A3,3,2);

>	seq(cat(A,i)=op(cat(A,i)),i=1..4);tvals;

Note that A2 and A4 have the same second part! So, now we repeat!

>	unassign('ans11');convert(sqrt(11),confrac,8,ans11);

>

ans11;

>

>