>

>

We first use modern computers to list a bunch of squares,  just to save headache! Traditionally these would be calculated as needed!

>	lis:=[seq(i^2,i=2..2500)];

$\mathrm{lis}:=\left[4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,324,361,400,441,484,529,576,625,676,729,784,841,900,961,1024,1089,1156,1225,1296,1369,1444,1521,1600,1681,1764,1849,1936,2025,2116,2209,2304,2401,2500,2601,2704,2809,2916,3025,3136,3249,3364,3481,3600,3721,3844,3969,4096,4225,4356,4489,4624,4761,4900,5041,5184,5329,5476,5625,5776,5929,6084,6241,6400,6561,6724,6889,7056,7225,7396,7569,7744,7921,8100,8281,8464,8649,8836,9025,9216,9409,9604,9801,10000,10201,10404,10609,10816,11025,11236,11449,11664,11881,12100,12321,12544,12769,12996,13225,13456,13689,13924,14161,14400,14641,14884,15129,15376,15625,15876,16129,16384,16641,16900,17161,17424,17689,17956,18225,18496,18769,19044,19321,19600,19881,20164,20449,20736,21025,21316,21609,21904,22201,22500,22801,23104,23409,23716,24025,24336,24649,24964,25281,25600,25921,26244,26569,26896,27225,27556,27889,28224,28561,28900,29241,29584,29929,30276,30625,30976,31329,31684,32041,32400,32761,33124,33489,33856,34225,34596,34969,35344,35721,36100,36481,36864,37249,37636,38025,38416,38809,39204,39601,40000,40401,40804,41209,41616,42025,42436,42849,43264,43681,44100,44521,44944,45369,45796,46225,46656,47089,47524,47961,48400,48841,49284,49729,50176,50625,51076,51529,51984,52441,52900,53361,53824,54289,54756,55225,55696,56169,56644,57121,57600,58081,58564,59049,59536,60025,60516,61009,61504,62001,62500,63001,63504,64009,64516,65025,65536,66049,66564,67081,67600,68121,68644,69169,69696,70225,70756,71289,71824,72361,72900,73441,73984,74529,75076,75625,76176,76729,77284,77841,78400,78961,79524,80089,80656,81225,81796,82369,82944,83521,84100,84681,85264,85849,86436,87025,87616,88209,88804,89401,90000,90601,91204,91809,92416,93025,93636,94249,94864,95481,96100,96721,97344,97969,98596,99225,99856,100489,101124,101761,102400,103041,103684,104329,104976,105625,106276,106929,107584,108241,108900,109561,110224,110889,111556,112225,112896,113569,114244,114921,115600,116281,116964,117649,118336,119025,119716,120409,121104,121801,122500,123201,123904,124609,125316,126025,126736,127449,128164,128881,129600,130321,131044,131769,132496,133225,133956,134689,135424,136161,136900,137641,138384,139129,139876,140625,141376,142129,142884,143641,144400,145161,145924,146689,147456,148225,148996,149769,150544,151321,152100,152881,153664,154449,155236,156025,156816,157609,158404,159201,160000,160801,161604,162409,163216,164025,164836,165649,166464,167281,168100,168921,169744,170569,171396,172225,173056,173889,174724,175561,176400,177241,178084,178929,179776,180625,181476,182329,183184,184041,184900,185761,186624,187489,188356,189225,190096,190969,191844,192721,193600,194481,195364,196249,197136,198025,198916,199809,200704,201601,202500,203401,204304,205209,206116,207025,207936,208849,209764,210681,211600,212521,213444,214369,215296,216225,217156,218089,219024,219961,220900,221841,222784,223729,224676,225625,226576,227529,228484,229441,230400,231361,232324,233289,234256,235225,236196,237169,238144,239121,240100,241081,242064,243049,244036,245025,246016,247009,248004,249001,250000,251001,252004,253009,254016,255025,256036,257049,258064,259081,260100,261121,262144,263169,264196,265225,266256,267289,268324,269361,270400,271441,272484,273529,274576,275625,276676,277729,278784,279841,280900,281961,283024,284089,285156,286225,287296,288369,289444,290521,291600,292681,293764,294849,295936,297025,298116,299209,300304,301401,302500,303601,304704,305809,306916,308025,309136,310249,311364,312481,313600,314721,315844,316969,318096,319225,320356,321489,322624,323761,324900,326041,327184,328329,329476,330625,331776,332929,334084,335241,336400,337561,338724,339889,341056,342225,343396,344569,345744,346921,348100,349281,350464,351649,352836,354025,355216,356409,357604,358801,360000,361201,362404,363609,364816,366025,367236,368449,369664,370881,372100,373321,374544,375769,376996,378225,379456,380689,381924,383161,384400,385641,386884,388129,389376,390625,391876,393129,394384,395641,396900,398161,399424,400689,401956,403225,404496,405769,407044,408321,409600,410881,412164,413449,414736,416025,417316,418609,419904,421201,422500,423801,425104,426409,427716,429025,430336,431649,432964,434281,435600,436921,438244,439569,440896,442225,443556,444889,446224,447561,448900,450241,451584,452929,454276,455625,456976,458329,459684,461041,462400,463761,465124,466489,467856,469225,470596,471969,473344,474721,476100,477481,478864,480249,481636,483025,484416,485809,487204,488601,490000,491401,492804,494209,495616,497025,498436,499849,501264,502681,504100,505521,506944,508369,509796,511225,512656,514089,515524,516961,518400,519841,521284,522729,524176,525625,527076,528529,529984,531441,532900,534361,535824,537289,538756,540225,541696,543169,544644,546121,547600,549081,550564,552049,553536,555025,556516,558009,559504,561001,562500,564001,565504,567009,568516,570025,571536,573049,574564,576081,577600,579121,580644,582169,583696,585225,586756,588289,589824,591361,592900,594441,595984,597529,599076,600625,602176,603729,605284,606841,608400,609961,611524,613089,614656,616225,617796,619369,620944,622521,624100,625681,627264,628849,630436,632025,633616,635209,636804,638401,640000,641601,643204,644809,646416,648025,649636,651249,652864,654481,656100,657721,659344,660969,662596,664225,665856,667489,669124,670761,672400,674041,675684,677329,678976,680625,682276,683929,685584,687241,688900,690561,692224,693889,695556,697225,698896,700569,702244,703921,705600,707281,708964,710649,712336,714025,715716,717409,719104,720801,722500,724201,725904,727609,729316,731025,732736,734449,736164,737881,739600,741321,743044,744769,746496,748225,749956,751689,753424,755161,756900,758641,760384,762129,763876,765625,767376,769129,770884,772641,774400,776161,777924,779689,781456,783225,784996,786769,788544,790321,792100,793881,795664,797449,799236,801025,802816,804609,806404,808201,810000,811801,813604,815409,817216,819025,820836,822649,824464,826281,828100,829921,831744,833569,835396,837225,839056,840889,842724,844561,846400,848241,850084,851929,853776,855625,857476,859329,861184,863041,864900,866761,868624,870489,872356,874225,876096,877969,879844,881721,883600,885481,887364,889249,891136,893025,894916,896809,898704,900601,902500,904401,906304,908209,910116,912025,913936,915849,917764,919681,921600,923521,925444,927369,929296,931225,933156,935089,937024,938961,940900,942841,944784,946729,948676,950625,952576,954529,956484,958441,960400,962361,964324,966289,968256,970225,972196,974169,976144,978121,980100,982081,984064,986049,988036,990025,992016,994009,996004,998001,1000000,1002001,1004004,1006009,1008016,1010025,1012036,1014049,1016064,1018081,1020100,1022121,1024144,1026169,1028196,1030225,1032256,1034289,1036324,1038361,1040400,1042441,1044484,1046529,1048576,1050625,1052676,1054729,1056784,1058841,1060900,1062961,1065024,1067089,1069156,1071225,1073296,1075369,1077444,1079521,1081600,1083681,1085764,1087849,1089936,1092025,1094116,1096209,1098304,1100401,1102500,1104601,1106704,1108809,1110916,1113025,1115136,1117249,1119364,1121481,1123600,1125721,1127844,1129969,1132096,1134225,1136356,1138489,1140624,1142761,1144900,1147041,1149184,1151329,1153476,1155625,1157776,1159929,1162084,1164241,1166400,1168561,1170724,1172889,1175056,1177225,1179396,1181569,1183744,1185921,1188100,1190281,1192464,1194649,1196836,1199025,1201216,1203409,1205604,1207801,1210000,1212201,1214404,1216609,1218816,1221025,1223236,1225449,1227664,1229881,1232100,1234321,1236544,1238769,1240996,1243225,1245456,1247689,1249924,1252161,1254400,1256641,1258884,1261129,1263376,1265625,1267876,1270129,1272384,1274641,1276900,1279161,1281424,1283689,1285956,1288225,1290496,1292769,1295044,1297321,1299600,1301881,1304164,1306449,1308736,1311025,1313316,1315609,1317904,1320201,1322500,1324801,1327104,1329409,1331716,1334025,1336336,1338649,1340964,1343281,1345600,1347921,1350244,1352569,1354896,1357225,1359556,1361889,1364224,1366561,1368900,1371241,1373584,1375929,1378276,1380625,1382976,1385329,1387684,1390041,1392400,1394761,1397124,1399489,1401856,1404225,1406596,1408969,1411344,1413721,1416100,1418481,1420864,1423249,1425636,1428025,1430416,1432809,1435204,1437601,1440000,1442401,1444804,1447209,1449616,1452025,1454436,1456849,1459264,1461681,1464100,1466521,1468944,1471369,1473796,1476225,1478656,1481089,1483524,1485961,1488400,1490841,1493284,1495729,1498176,1500625,1503076,1505529,1507984,1510441,1512900,1515361,1517824,1520289,1522756,1525225,1527696,1530169,1532644,1535121,1537600,1540081,1542564,1545049,1547536,1550025,1552516,1555009,1557504,1560001,1562500,1565001,1567504,1570009,1572516,1575025,1577536,1580049,1582564,1585081,1587600,1590121,1592644,1595169,1597696,1600225,1602756,1605289,1607824,1610361,1612900,1615441,1617984,1620529,1623076,1625625,1628176,1630729,1633284,1635841,1638400,1640961,1643524,1646089,1648656,1651225,1653796,1656369,1658944,1661521,1664100,1666681,1669264,1671849,1674436,1677025,1679616,1682209,1684804,1687401,1690000,1692601,1695204,1697809,1700416,1703025,1705636,1708249,1710864,1713481,1716100,1718721,1721344,1723969,1726596,1729225,1731856,1734489,1737124,1739761,1742400,1745041,1747684,1750329,1752976,1755625,1758276,1760929,1763584,1766241,1768900,1771561,1774224,1776889,1779556,1782225,1784896,1787569,1790244,1792921,1795600,1798281,1800964,1803649,1806336,1809025,1811716,1814409,1817104,1819801,1822500,1825201,1827904,1830609,1833316,1836025,1838736,1841449,1844164,1846881,1849600,1852321,1855044,1857769,1860496,1863225,1865956,1868689,1871424,1874161,1876900,1879641,1882384,1885129,1887876,1890625,1893376,1896129,1898884,1901641,1904400,1907161,1909924,1912689,1915456,1918225,1920996,1923769,1926544,1929321,1932100,1934881,1937664,1940449,1943236,1946025,1948816,1951609,1954404,1957201,1960000,1962801,1965604,1968409,1971216,1974025,1976836,1979649,1982464,1985281,1988100,1990921,1993744,1996569,1999396,2002225,2005056,2007889,2010724,2013561,2016400,2019241,2022084,2024929,2027776,2030625,2033476,2036329,2039184,2042041,2044900,2047761,2050624,2053489,2056356,2059225,2062096,2064969,2067844,2070721,2073600,2076481,2079364,2082249,2085136,2088025,2090916,2093809,2096704,2099601,2102500,2105401,2108304,2111209,2114116,2117025,2119936,2122849,2125764,2128681,2131600,2134521,2137444,2140369,2143296,2146225,2149156,2152089,2155024,2157961,2160900,2163841,2166784,2169729,2172676,2175625,2178576,2181529,2184484,2187441,2190400,2193361,2196324,2199289,2202256,2205225,2208196,2211169,2214144,2217121,2220100,2223081,2226064,2229049,2232036,2235025,2238016,2241009,2244004,2247001,2250000,2253001,2256004,2259009,2262016,2265025,2268036,2271049,2274064,2277081,2280100,2283121,2286144,2289169,2292196,2295225,2298256,2301289,2304324,2307361,2310400,2313441,2316484,2319529,2322576,2325625,2328676,2331729,2334784,2337841,2340900,2343961,2347024,2350089,2353156,2356225,2359296,2362369,2365444,2368521,2371600,2374681,2377764,2380849,2383936,2387025,2390116,2393209,2396304,2399401,2402500,2405601,2408704,2411809,2414916,2418025,2421136,2424249,2427364,2430481,2433600,2436721,2439844,2442969,2446096,2449225,2452356,2455489,2458624,2461761,2464900,2468041,2471184,2474329,2477476,2480625,2483776,2486929,2490084,2493241,2496400,2499561,2502724,2505889,2509056,2512225,2515396,2518569,2521744,2524921,2528100,2531281,2534464,2537649,2540836,2544025,2547216,2550409,2553604,2556801,2560000,2563201,2566404,2569609,2572816,2576025,2579236,2582449,2585664,2588881,2592100,2595321,2598544,2601769,2604996,2608225,2611456,2614689,2617924,2621161,2624400,2627641,2630884,2634129,2637376,2640625,2643876,2647129,2650384,2653641,2656900,2660161,2663424,2666689,2669956,2673225,2676496,2679769,2683044,2686321,2689600,2692881,2696164,2699449,2702736,2706025,2709316,2712609,2715904,2719201,2722500,2725801,2729104,2732409,2735716,2739025,2742336,2745649,2748964,2752281,2755600,2758921,2762244,2765569,2768896,2772225,2775556,2778889,2782224,2785561,2788900,2792241,2795584,2798929,2802276,2805625,2808976,2812329,2815684,2819041,2822400,2825761,2829124,2832489,2835856,2839225,2842596,2845969,2849344,2852721,2856100,2859481,2862864,2866249,2869636,2873025,2876416,2879809,2883204,2886601,2890000,2893401,2896804,2900209,2903616,2907025,2910436,2913849,2917264,2920681,2924100,2927521,2930944,2934369,2937796,2941225,2944656,2948089,2951524,2954961,2958400,2961841,2965284,2968729,2972176,2975625,2979076,2982529,2985984,2989441,2992900,2996361,2999824,3003289,3006756,3010225,3013696,3017169,3020644,3024121,3027600,3031081,3034564,3038049,3041536,3045025,3048516,3052009,3055504,3059001,3062500,3066001,3069504,3073009,3076516,3080025,3083536,3087049,3090564,3094081,3097600,3101121,3104644,3108169,3111696,3115225,3118756,3122289,3125824,3129361,3132900,3136441,3139984,3143529,3147076,3150625,3154176,3157729,3161284,3164841,3168400,3171961,3175524,3179089,3182656,3186225,3189796,3193369,3196944,3200521,3204100,3207681,3211264,3214849,3218436,3222025,3225616,3229209,3232804,3236401,3240000,3243601,3247204,3250809,3254416,3258025,3261636,3265249,3268864,3272481,3276100,3279721,3283344,3286969,3290596,3294225,3297856,3301489,3305124,3308761,3312400,3316041,3319684,3323329,3326976,3330625,3334276,3337929,3341584,3345241,3348900,3352561,3356224,3359889,3363556,3367225,3370896,3374569,3378244,3381921,3385600,3389281,3392964,3396649,3400336,3404025,3407716,3411409,3415104,3418801,3422500,3426201,3429904,3433609,3437316,3441025,3444736,3448449,3452164,3455881,3459600,3463321,3467044,3470769,3474496,3478225,3481956,3485689,3489424,3493161,3496900,3500641,3504384,3508129,3511876,3515625,3519376,3523129,3526884,3530641,3534400,3538161,3541924,3545689,3549456,3553225,3556996,3560769,3564544,3568321,3572100,3575881,3579664,3583449,3587236,3591025,3594816,3598609,3602404,3606201,3610000,3613801,3617604,3621409,3625216,3629025,3632836,3636649,3640464,3644281,3648100,3651921,3655744,3659569,3663396,3667225,3671056,3674889,3678724,3682561,3686400,3690241,3694084,3697929,3701776,3705625,3709476,3713329,3717184,3721041,3724900,3728761,3732624,3736489,3740356,3744225,3748096,3751969,3755844,3759721,3763600,3767481,3771364,3775249,3779136,3783025,3786916,3790809,3794704,3798601,3802500,3806401,3810304,3814209,3818116,3822025,3825936,3829849,3833764,3837681,3841600,3845521,3849444,3853369,3857296,3861225,3865156,3869089,3873024,3876961,3880900,3884841,3888784,3892729,3896676,3900625,3904576,3908529,3912484,3916441,3920400,3924361,3928324,3932289,3936256,3940225,3944196,3948169,3952144,3956121,3960100,3964081,3968064,3972049,3976036,3980025,3984016,3988009,3992004,3996001,4000000,4004001,4008004,4012009,4016016,4020025,4024036,4028049,4032064,4036081,4040100,4044121,4048144,4052169,4056196,4060225,4064256,4068289,4072324,4076361,4080400,4084441,4088484,4092529,4096576,4100625,4104676,4108729,4112784,4116841,4120900,4124961,4129024,4133089,4137156,4141225,4145296,4149369,4153444,4157521,4161600,4165681,4169764,4173849,4177936,4182025,4186116,4190209,4194304,4198401,4202500,4206601,4210704,4214809,4218916,4223025,4227136,4231249,4235364,4239481,4243600,4247721,4251844,4255969,4260096,4264225,4268356,4272489,4276624,4280761,4284900,4289041,4293184,4297329,4301476,4305625,4309776,4313929,4318084,4322241,4326400,4330561,4334724,4338889,4343056,4347225,4351396,4355569,4359744,4363921,4368100,4372281,4376464,4380649,4384836,4389025,4393216,4397409,4401604,4405801,4410000,4414201,4418404,4422609,4426816,4431025,4435236,4439449,4443664,4447881,4452100,4456321,4460544,4464769,4468996,4473225,4477456,4481689,4485924,4490161,4494400,4498641,4502884,4507129,4511376,4515625,4519876,4524129,4528384,4532641,4536900,4541161,4545424,4549689,4553956,4558225,4562496,4566769,4571044,4575321,4579600,4583881,4588164,4592449,4596736,4601025,4605316,4609609,4613904,4618201,4622500,4626801,4631104,4635409,4639716,4644025,4648336,4652649,4656964,4661281,4665600,4669921,4674244,4678569,4682896,4687225,4691556,4695889,4700224,4704561,4708900,4713241,4717584,4721929,4726276,4730625,4734976,4739329,4743684,4748041,4752400,4756761,4761124,4765489,4769856,4774225,4778596,4782969,4787344,4791721,4796100,4800481,4804864,4809249,4813636,4818025,4822416,4826809,4831204,4835601,4840000,4844401,4848804,4853209,4857616,4862025,4866436,4870849,4875264,4879681,4884100,4888521,4892944,4897369,4901796,4906225,4910656,4915089,4919524,4923961,4928400,4932841,4937284,4941729,4946176,4950625,4955076,4959529,4963984,4968441,4972900,4977361,4981824,4986289,4990756,4995225,4999696,5004169,5008644,5013121,5017600,5022081,5026564,5031049,5035536,5040025,5044516,5049009,5053504,5058001,5062500,5067001,5071504,5076009,5080516,5085025,5089536,5094049,5098564,5103081,5107600,5112121,5116644,5121169,5125696,5130225,5134756,5139289,5143824,5148361,5152900,5157441,5161984,5166529,5171076,5175625,5180176,5184729,5189284,5193841,5198400,5202961,5207524,5212089,5216656,5221225,5225796,5230369,5234944,5239521,5244100,5248681,5253264,5257849,5262436,5267025,5271616,5276209,5280804,5285401,5290000,5294601,5299204,5303809,5308416,5313025,5317636,5322249,5326864,5331481,5336100,5340721,5345344,5349969,5354596,5359225,5363856,5368489,5373124,5377761,5382400,5387041,5391684,5396329,5400976,5405625,5410276,5414929,5419584,5424241,5428900,5433561,5438224,5442889,5447556,5452225,5456896,5461569,5466244,5470921,5475600,5480281,5484964,5489649,5494336,5499025,5503716,5508409,5513104,5517801,5522500,5527201,5531904,5536609,5541316,5546025,5550736,5555449,5560164,5564881,5569600,5574321,5579044,5583769,5588496,5593225,5597956,5602689,5607424,5612161,5616900,5621641,5626384,5631129,5635876,5640625,5645376,5650129,5654884,5659641,5664400,5669161,5673924,5678689,5683456,5688225,5692996,5697769,5702544,5707321,5712100,5716881,5721664,5726449,5731236,5736025,5740816,5745609,5750404,5755201,5760000,5764801,5769604,5774409,5779216,5784025,5788836,5793649,5798464,5803281,5808100,5812921,5817744,5822569,5827396,5832225,5837056,5841889,5846724,5851561,5856400,5861241,5866084,5870929,5875776,5880625,5885476,5890329,5895184,5900041,5904900,5909761,5914624,5919489,5924356,5929225,5934096,5938969,5943844,5948721,5953600,5958481,5963364,5968249,5973136,5978025,5982916,5987809,5992704,5997601,6002500,6007401,6012304,6017209,6022116,6027025,6031936,6036849,6041764,6046681,6051600,6056521,6061444,6066369,6071296,6076225,6081156,6086089,6091024,6095961,6100900,6105841,6110784,6115729,6120676,6125625,6130576,6135529,6140484,6145441,6150400,6155361,6160324,6165289,6170256,6175225,6180196,6185169,6190144,6195121,6200100,6205081,6210064,6215049,6220036,6225025,6230016,6235009,6240004,6245001,6250000\right]$

>	ch:=proc(n,t,s) local ans,tmp; if n<>t^2-s then return(`bad start`); fi; ans:=[n,t+1,s+2*t+1]; if member(ans[3],lis) then print('success') else print('fails',evalf[2](t+1-sqrt(ans[3])));fi; op(ans);end;

>

chh:=proc(n,t,s) local ans,tmp,ct; if n<>t^2-s then return(`bad start`); fi; if type(n,even) then RETURN("Must have odd number",n):fi: ans:=[n,t+1,s+2*t+1]; for ct from 1 to 2000 do; if ans[2]>n-2 then RETURN("It is prime",n);fi: if (member(ans[3],lis)) then return(`success`,ans[1],ans[2]+sqrt(ans[3]),ans[2]-sqrt(ans[3])); fi; #print(member(ans[3],lis)); ans:=[ans[1],ans[2]+1,ans[3]+2*ans[2]+1]; #print(ans,ct); od; print(`it is prime`);ans; end;

>

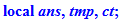
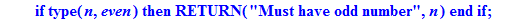
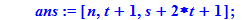
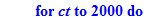
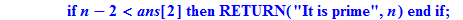
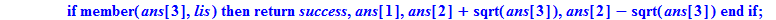
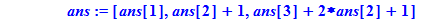
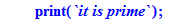
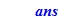
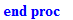
ch2:=proc(n,t,s,m) local ans,tmp,ct; if n<>t^2-s then return(`bad start`); fi; if type(n,even) then RETURN("Must have odd number",n):fi: ans:=[n,t+1,s+2*t+1]; for ct from 1 to m do; if ans[2]>n-2 then RETURN("It is prime",n);fi: if (member(ans[3],lis)) then return(`success`,ans[1],ans[2]+sqrt(ans[3]),ans[2]-sqrt(ans[3])); fi; if ct>2500 then RETURN("Limit of 2500 exceeded",ct):fi: #print(member(ans[3],lis)); ans:=[ans[1],ans[2]+1,ans[3]+2*ans[2]+1]; #print(ans,ct); od; print(`it is prime`);ans; end;

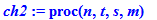
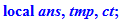
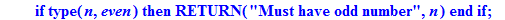
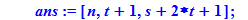
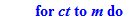
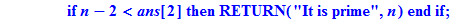
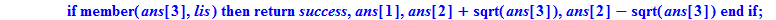
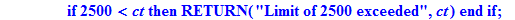
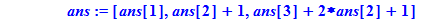
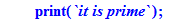
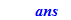
>	tch:=proc(n) local t,s; t:=ceil(sqrt(n));s:=t^2-n; ch2(n,t,s,n);end:

>

tch(123);

$\mathrm{success},123,41,3$

>

>	tch(4211);ifactor(4211);

Error, (in ch2) invalid input: member received lis, which is not valid for its 2nd argument, s

$\left(4211\right)$

>

tch(127);

$\mathrm{success},127,127,1$

>	ifactor(4211);

$\left(4211\right)$

>

tch(127);

$\mathrm{success},127,127,1$

>

tch(129);

$\mathrm{success},129,43,3$

>

tch(131);

$\mathrm{success},131,131,1$

>	tch(2^17+1);

$\text{Limit of 2500 exceeded},2501$

>

#

>	tch(23111);

$\mathrm{success},23111,191,121$

>