Theorem 20.3: The circumference C of
a circle of radius r is
Figure 21.2: Hyperbolic Circle
In Euclidean geometry 
where 
is
the perimeter of the regular n-gon inscribed in the circle.
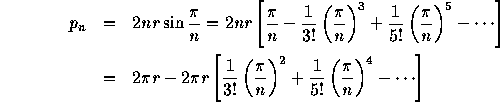
Thus, 
.
In hyperbolic geometry we can still compute the perimeter and compute the limit, but we will use Theorem 21.1 to compute the perimeter.
The proof is nothing but the following computation.
Let K be the area of 
, so that according to our choices, with
k=1 and angles measured in radians, 
. Let
have a right angle at C, then 
.
Once again the proof is a computation.
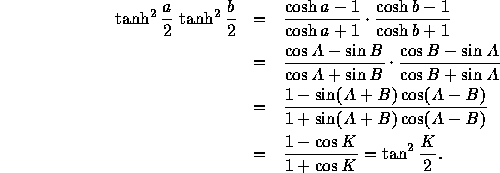
Using this and our limiting approach we can now compute the area of a circle.
Theorem 20.5: The area, A, of a circle of radius r is
Proof:
We do this just as before. If 
is the area of the inscribed regular
n-gon, then 
. In the right triangle
in Figure 21.2 let K, a, and p denote , 
and .
The area of the right triangle is 
.
Thus, we find that
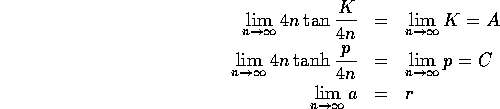
Putting all of this together we have that
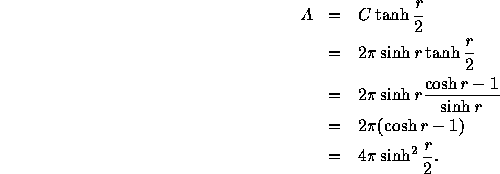
Thus, we have computed the area of a circle.
.