Peano's Axioms

The following is quoted from Edmund Landau, Foundations of Analysis, Chelsea, 1951, pp. 1-18.

We assume the following to be given:

A set (i.e. totality) of objects called natural numbers, possessing the properties--called axioms--to be listed below.

Before formulating the axioms we make some remarks about the symbols = and 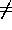which will be used.

Unless otherwise specified, small italic letters will stand for natural numbers...

If x is given and y is given, then

either x and y are the same number; this may be written x=y (= to be read ``equals'');

or x and y are not the same number; this may be written 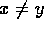( 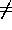to be read ``is not equal to'').

Accordingly, the following are true on purely logical grounds:

1. x=x for every x.
2. If x=y then y=x.
3. If x=y, y=z then x=z.

Thus a statement such as a=b=c=d, which on the face of it means merely that a=b, b=c, c=d, contains the additional information that, say, a=c, a=d, b=d....

Now, we assume that the set of all natural numbers has the following properties:

Axiom 1:

1 is a natural number. That is, our set is not empty; it contains an object called 1 (read ``one'').

Axiom 2:

For each x there exists exactly one natural number, called the successor of x, which will be denoted by x'.

Axiom 3:

We always have 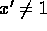. That is, there exists no number whose successor is 1. That is, there exists no number whose successor is 1.

Axiom 4:

If x'=y' then x=y. That is, for any given number there exists either no number or exactly one number whose successor is the given number.

Axiom 5 (Axiom of Induction):

Let there be given a set M of natural numbers, with the following properties:

I.

1 belongs to M.

II.

If x belongs to M then so does x'.

Then M contains all the natural numbers.

Notice that there is no mention of such things as addition or multiplication. How are these to be defined?