


Next: Comments on Hilbert's Program
Up: The Natural Numbers
Previous: Peano's Axioms
The following is quoted from
Edmund Landau, Foundations of Analysis, Chelsea, 1951,
pp. 1-18.
- Theorem 1:
- If
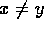 then
then 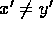 .
.
- Theorem 2:
-
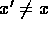 .
.
- Theorem 3:
- If
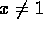 there exists one (and hence,
by Axiom 4, exactly one) u such that x=u'.
there exists one (and hence,
by Axiom 4, exactly one) u such that x=u'.
- Theorem 4,
- and at the same time Definition 1:
To every pair of numbers
x,y, we may assign in exactly one way a natural number, called x+y
(+ to be read ``plus''),
such that
- 1.
- x+1=x' for every x.
- 2.
- x+y'=(x+y)' for every x and every y.
x+y is called the sum of x and y, or the number obtained by
addition of y to x.
- Theorem 5 (Associative Law of Addition):
- (x+y)+z=x+(y+z).
- Theorem 6 (Commutative Law of Addition):
- x+y=y+x.
- Theorem 7:
-
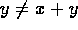 .
.
- Theorem 8:
- If
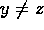 then
then 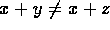 .
.
- Theorem 9:
- For given x and y, exactly one of the
following must be the case:
- 1.
- x=y.
- 2.
- There exists a u (exactly one, by Theorem 8) such that
x=y+u.
- 3.
- There exists a v (exactly one, by Theorem 8) such that
y=x+v.
- Definition 2:
- If x=y+u then x>y. (> to be read ``is
greater than.'')
- Definition 3:
- If y=x+v then x<y. (< to be read ``is
less than.'')
- Theorem 10:
- For any given x,y, we have exactly one of
the cases x=y, x>y, x<y.
- Theorem 11:
- If x>y then y<x.
- Theorem 12:
- If x<y then y>x.
- Definition 4:
-
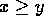 means x>y or x=y. (
means x>y or x=y. ( 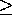 to be
read ``is greater than or equal to.'')
to be
read ``is greater than or equal to.'')
- Definition 5:
-
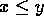 means x<y or x=y. (
means x<y or x=y. (  to be
read ``is less than or equal to.'')
to be
read ``is less than or equal to.'')
- Theorem 13:
- If
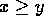 then
then 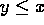 .
.
- Theorem 14:
- If
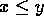 then
then 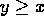 .
.
- Theorem 15 (Transitivity of Ordering:)
- If x<y,
y<z, then x<z.
- Theorem 16:
- If
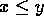 , y<z or x<y,
, y<z or x<y, 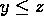 ,
then x<z.
,
then x<z.
- Theorem 17:
- If
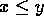 ,
, 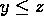 , then
, then 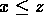 .
.
- Theorem 18:
- x+y>x.
- Theorem 19:
- If x>y, or x=y, or x<y, then
x+z>y+z, or x+z=y+z, or x+z<y+z, respectively.
- Theorem 20:
- If x+z>y+z, or x+z=y+z, or x+z<y+z,
then x>y, or x=y, or x<y, respectively.
- Theorem 21:
- If x>y, z>u, then x+z>y+u.
- Theorem 22:
- If
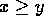 , z>u or x>y,
, z>u or x>y, 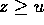 ,
then x+z>y+u.
,
then x+z>y+u.
- Theorem 23:
- If
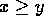 ,
, 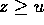 , then
, then 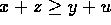 .
.
- Theorem 24:
-
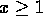 .
.
- Theorem 25:
- If y>x then
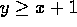 .
.
- Theorem 26:
- If y<x+1 then
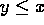 .
.
- Theorem 27:
- In every non-empty set of natural numbers
there is a least one (i.e., one which is less than any other number of
the set).
- Theorem 28
- and at the same time Definition 6: To every pair of
numbers x,y, we may assign in exactly one way a natural number,
called
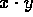 (
(  to be read ``times''; however, the dot is
usually omitted), such that
to be read ``times''; however, the dot is
usually omitted), such that
- 1.
-
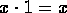 for every x,
for every x,
- 2.
-
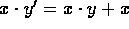 for every x and every y.
for every x and every y.
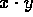 is called the product of x and y, or the number obtained
from multiplication of x by y.
is called the product of x and y, or the number obtained
from multiplication of x by y.
- Theorem 29 (Commutative Law of Multiplication):
-
xy=yx.
- Theorem 30 (Distributive Law):
- x(y+z)=xy+xz.
- Theorem 31 (Associative Law of Multiplication):
-
(xy)z=x(yz).
- Theorem 32:
- If x>y, or x=y, or x<y, then
xz>yz, xz=yz, or xz<yz, respectively.
- Theorem 33:
- If xz>yz, or xz=yz, or xz<yz, then
x>y, or x=y, or x<y, respectively.
- Theorem 34:
- If x>y, z>u, then xz>yu.
- Theorem 35:
- If
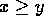 , z>u or x>y,
, z>u or x>y, 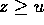 ,
then xz>yu.
,
then xz>yu.
- Theorem 36:
- If
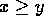 ,
, 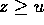 , then
, then 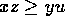 .
.



Next: Comments on Hilbert's Program
Up: The Natural Numbers
Previous: Peano's Axioms
Carl Lee
Wed Sep 16 09:26:16 EDT 1998
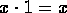 for every x,
for every x,
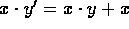 for every x and every y.
for every x and every y.