next up previous
Next: Isomorphism Up: Relations and Functions Previous: The Pigeonhole Principle

Equivalence Relations

Now back to relations. Sometimes, to make notation easier, we may write 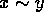tex2html_wrap_inline571 instead of 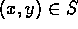tex2html_wrap_inline573 for a relation S.

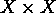Suppose S is a relation between X and itself; i.e., a subset of tex2html_wrap_inline581 . S is called an equivalence relation if the following three properties hold:

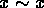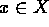  1. Reflexive Property: tex2html_wrap_inline585 for every tex2html_wrap_inline587 .
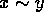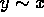  2. Symmetric Property: If tex2html_wrap_inline571 then tex2html_wrap_inline591 .
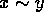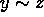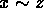  3. Transitive Property: If tex2html_wrap_inline571 and tex2html_wrap_inline595 then tex2html_wrap_inline597 .

Which of the following are equivalence relations? Why or why not?

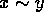  1. X is the set of real numbers, and tex2html_wrap_inline571 if and only if x actually equals y.
  2. X is the set of all real numbers, and 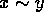tex2html_wrap_inline571 if and only if x<y.
  3. X is the set of integers, and n is a fixed positive integer. 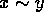tex2html_wrap_inline571 if and only if n is a divisor of y-x.
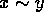  4. X is the set of all natural numbers, and tex2html_wrap_inline571 if and only if the fraction x/y, when ``reduced'' becomes a fraction a/b in which both the numerator and the denominator are odd.
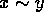  5. X is the set of all natural numbers, and tex2html_wrap_inline571 if and only if x and y have no common divisor greater than 1.
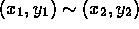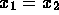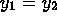  6. X is the set of ordered pairs of integers, and tex2html_wrap_inline643 if and only if tex2html_wrap_inline645 and tex2html_wrap_inline647 .
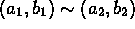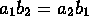  7. X is the set of all ordered pairs (a,b) of integers, and tex2html_wrap_inline653 if and only if tex2html_wrap_inline655 .
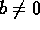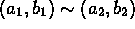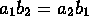  8. X is the set of all ordered pairs (a,b) of integers for which tex2html_wrap_inline661 , and tex2html_wrap_inline653 if and only if tex2html_wrap_inline655 .
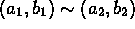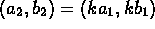  9. X is the set of all ordered pairs (a,b) of real numbers, excluding the ordered pair (0,0), and tex2html_wrap_inline653 if and only if there is a nonzero real number k such that tex2html_wrap_inline677 .
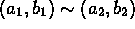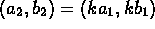  10. X is the set of all ordered pairs (a,b) of real numbers, and tex2html_wrap_inline653 if and only if there is a real number k such that tex2html_wrap_inline677 .

Whenever you have an equivalence relation on a set X, you can partition the elements of X into subsets, such that a is in subset T if and only if T consists of all elements of X equivalent to a. These subsets are called the equivalence classes of the equivalence relation. Conversely, whenever you have a partition of a set X into the union of mutually disjoint subsets, then you can define a equivalence relation on X by declaring 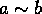tex2html_wrap_inline707 if and only if a and b belong to the same subset of the partition. (Try to prove these statements.)

next up previous
Next: Isomorphism Up: Relations and Functions Previous: The Pigeonhole Principle

Carl Lee
Wed Sep 30 08:36:10 EDT 1998