Consider the following game: Write the numbers from 1 to 9 on a piece of paper. Two players take turns marking the numbers one at a time; for example, the first player could draw circles around his/her numbers, and the second player could draw squares. The game ends when one of the players has, among his/her marked numbers, a subset of size exactly three that sums to 15.
It turns out that this game is isomorphic to tic-tac-toe. You can see
this by placing the numbers from 1 to 9 in the cells of a
tic-tac-toe board in the following way (corresponding to a 
magic square):
The ways to get three-in-a-row in tic-tac-toe correspond exactly to the ways to select three numbers that sum to 15.
In the next section, we will construct number systems that are isomorphic to our familiar ones. In fact, we can use these constructions as the definitions of the number systems.
Isomorphism is a crucial, fundamental concept in mathematics. Loosely speaking, two structures are isomorphic if there is a one-to-one correspondence between their respective components so that any relationship or property that holds among a subset of components of the first structure must hold among the corresponding components of the corresponding subset of the second structure, and vice versa.
For example, suppose I have a subset 
and I choose to
define two operations, 
and 
, in the following way:
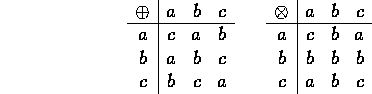
Can you prove that this is isomorphic to 
integers modulo 3?
Define a function f from X to by f(a)=2, f(b)=0,
and f(c)=1. Then we have to verify that 
in X if and
only if f(x)+f(y)=f(z) in , and 
in X if and
only if 
in . Another way of expressing
this is:
