Using Equivalence Relations to Define Number Systems

``God made the integers; all else is the work of man.'' --Kronecker

1. The Integers. X is the set of ordered pairs (a,b) of natural numbers. Define equivalence by

   

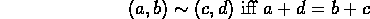
   Denote the equivalence class containing (a,b) by [(a,b)] Define addition by

   

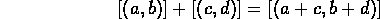
   Define multiplication by

   

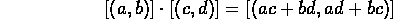
2. The Integers Modulo n. X is the set of integers, and n is a fixed integer. Define equivalence by

   

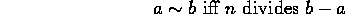
   Denote the equivalence class containing a by [a]. Define addition by

   

   Define multiplication by

   

3. The Rational Numbers. X is the set of ordered pairs (a,b) of integers, where 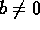. Define equivalence by

   

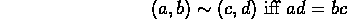
   Denote the equivalence class containing (a,b) by [(a,b)]. Define addition by

   

   Define multiplication by

   

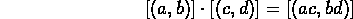
4. The Real Numbers. First, some definitions. Consider a sequence 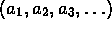of rational numbers. To say that this sequence converges to a rational number L means for every positive rational number there exists a positive integer N such that n>N implies that 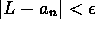; i.e., the terms of the sequence get arbitrarily close to L. To say that this sequence is a Cauchy sequence means that for every positive rational number there exists a positive integer N such that m,n>N implies 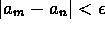; i.e., the terms of the sequence get arbitrarily close to each other.

   Let X be the set of Cauchy sequences 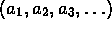of rational numbers. Define equivalence by

   

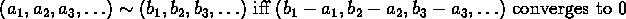
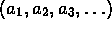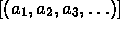   Denote the equivalence class containing by . Define addition by

   

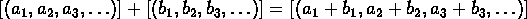
   Define multiplication by

   

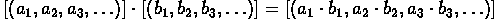
5. The Complex Numbers. X is the set of ordered pairs (a,b) of real numbers. Define equivalence by

   

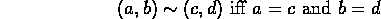
   Denote the equivalence class containing (a,b) by [(a,b)]. Define addition by

   

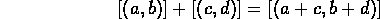
   Define multiplication by

   

In each of the above cases, you should be able to verify that

1. The relation is indeed an equivalence relation.
2. The two operations are well-defined; i.e., the sum or product is in the set, and the sum or product does not depend upon which representatives of the equivalence classes are added or multiplied.
3. There is an additive and a multiplicative identity.
4. Addition and multiplication are commutative and associative.
5. The distributive law of multiplication over addition holds.
6. Additive and multiplicative inverses exist when you expect them to.

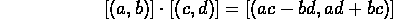
Are you convinced that each of the above structures is isomorphic to the number systems as we usually envision them?