


Next: Explorations with Clusters and
Up: PolygonsPatterns, and Polyhedra
Previous: A Very Small Collection
- Regular polygons.
- Give a definition of a regular polygon.
- How can a regular n-gon be constructed with a ruler and protractor?
- What is the measure of an interior angle of a regular n-gon?
- Of a central angle?
- Of an exterior angle?
- Angle sums.
- What is the sum of the central angles of a regular polygon?
- Exterior angle sums.
- What is the sum of the exterior angles of a regular polygon?
- Does this result still hold if the polygon is not regular?
- Interior angle sums.
- What is the sum of the interior angles of a regular n-gon?
- Does this result still hold if the polygon is not regular but is still
convex?
- What if the polygon is not even convex?
- Show how a convex n-gon can be subdivided into n-2
triangles.
- Can any (not necessarily convex) n-gon be subdivided into
n-2 triangles?
- What might be a good definition for a three-dimensional analogue
of a regular polygon?
- Inscribe a regular n-polygon in a circle of radius one centered at the
origin, with one vertex of the polygon at the point (1,0).
- If n=4, what are the coordinates of the other three vertices?
- Equilateral triangles.
- If n=3, what are the coordinates of the other two vertices?
- Suppose one of these two vertices has coordinates (a,b).
What is
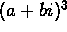 ? Why?
? Why?
- General regular n-gons.
- For general n, what are the coordinates of the other n-1 vertices?
- Suppose one of these vertices has coordinates (a,b).
What can you say about
powers of a+bi? Why?
- Find all the complex numbers solving
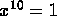 ,
, - For general n, what is the area of the n-gon?
- What is the perimeter? Use this to approximate
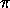 .
. - Cut up the polygon into triangles centered at the origin
and rearrange them to guess/motivate the formula for the area of a circle.
- Operations with complex numbers.
- Explain how to add and multiply complex numbers geometrically.
- What is the connection with the angle sum formulas for sine and
cosine?
- Give a geometrical interpretation for the square root of -1.
- Find the 3rd roots of i.
- Find the 10th roots of i.
- How can you find all the nth roots of a general complex number a+bi?



Next: Explorations with Clusters and
Up: PolygonsPatterns, and Polyhedra
Previous: A Very Small Collection
Carl Lee
Wed Nov 4 12:13:22 EST 1998
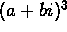 ? Why?
? Why?
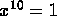 ,
,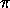 .
.