Explorations with Clusters and Tilings

1. Edge-to-edge tilings.
   1. Can the plane be tiled with equilateral triangles, meeting edge-to-edge?
   2. What about other regular n-gons?
2. Non edge-to-edge tilings.
   1. Can the plane be tiled by equilateral triangles, where not all of them meet edge-to-edge?
   2. Where none of them meet edge-to-edge?
   3. What about the same questions for squares?
   4. For other polygons?
3. Tiling with polyhedra.
   1. Can space be tiled with regular tetrahedra, meeting face to face?
   2. What about cubes?
   3. What about other polyhedra?
4. Tilings with congruent tiles.
   1. For which triangles is it true that you can tile the plane with multiple congruent copies of itself?
   2. For which quadrilaterals?
   3. For which pentagons?
   4. For which hexagons?
   5. For the above questions, in which cases can this be done so that the same number of polygons meet at each vertex also?
5. ``Escher-like'' tilings.
   1. Modify some of the polygons in the above tilings to get more complicated shapes for which the plane can be tiled with congruent copies.
6. A planar cluster is a group of regular polygons (not necessarily all of the same type) meeting edge-to-edge tightly around a common vertex in the plane.
   1. Make a list of all possible clusters.
   2. How do you know you have them all?
   3. Which clusters can be extended to a tiling of the plane so that the same cluster (i.e., the same number of polygons of each type, meeting in the same cyclic order) occurs around each vertex? Draw a good picture of each such tiling.
   4. Determine possible coordinates of the vertices of each of these tilings.
7. A space cluster is a group of regular polygons (not necessarily all of the same type) meeting edge-to-edge around a common vertex, but such that the sum of the interior angles is less than 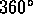, so that the cluster is not planar.
   1. Make a list of all possible clusters.
   2. How do you know you have them all?
   3. Which clusters can be extended to the boundary of a polyhedron so that the same cluster (i.e., the same number of polygons of each type, meeting in the same cyclic order) occurs around each vertex? Draw a good picture and/or make a model of each such polyhedron.