


Next: About this document
Up: PolygonsPatterns, and Polyhedra
Previous: Explorations with Clusters and
A rigid motion of the plane 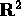 is a
function
is a
function 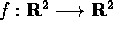 such that for any two points
p and q in the plane, the distance between f(p) and f(q) equals the
distance between p and q. We will (I hope) prove that besides the
identity map f(p)=p, there are only four different types of rigid
motions: translations, rotations about points, reflections across
lines, and glide reflections (a reflection across a line followed by a
translation parallel to the line). Notice that a translation by a
distance of 0 is the identity map, as is a rotation by an angle that is
an integer multiple of
such that for any two points
p and q in the plane, the distance between f(p) and f(q) equals the
distance between p and q. We will (I hope) prove that besides the
identity map f(p)=p, there are only four different types of rigid
motions: translations, rotations about points, reflections across
lines, and glide reflections (a reflection across a line followed by a
translation parallel to the line). Notice that a translation by a
distance of 0 is the identity map, as is a rotation by an angle that is
an integer multiple of 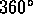 . Also a glide reflection involving a
translation by a distance of 0 is simply a reflection.
. Also a glide reflection involving a
translation by a distance of 0 is simply a reflection.
Given any subset S of the plane, a symmetry of S is a
rigid motion f of 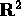 such that f(S)=S. This doesn't mean that every
point of the subset is fixed by f, but that
such that f(S)=S. This doesn't mean that every
point of the subset is fixed by f, but that 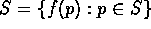 ;
i.e., every point in S is mapped to a point in S, and every point
in S is the image of some point in S.
;
i.e., every point in S is mapped to a point in S, and every point
in S is the image of some point in S.
Consider the set 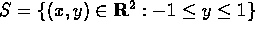 . We will call
this a strip. What are the possible symmetries of the strip?
. We will call
this a strip. What are the possible symmetries of the strip?
- The identity motion, which we will denote I.
- Translations by any amount parallel to the x-axis. If we
translate by an amount a (which may be positive, negative, or zero),
we will denote this symmetry by
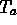 .
. - Rotations by
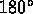 about a point on the x-axis. If we
rotate about the point (b,0) we will denote this symmetry by
about a point on the x-axis. If we
rotate about the point (b,0) we will denote this symmetry by
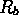 .
. - Vertical reflection across any line perpendicular to the
x-axis. If we reflect across the line x=c, we will denote this
symmetry by
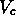 .
. - Horizontal reflection across the x-axis, which we will denote
H.
- Glide reflection across the x-axis. If we reflect across the
x-axis and then translate by an amount d (which may be positive,
negative, or zero), we will denote this symmetry by
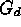 .
.
A repeating strip pattern is a subset of the above strip such
that each of its translational symmetries is a repetition (positive,
negative, or zero) of one particular translational symmetry.
- For each of the strip symmetries, write a formula for the
function.
- I(x,y)=(x,y).
-
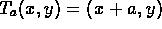 .
. -
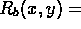
-
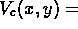
- H(x,y)=
-
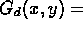
- For each of the following strip symmetries, write the formula:
- A translation to the right by 2 units.
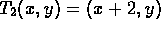 .
. - A translation to the left by 3 units.
- A rotation by
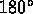 about the point (-5,0).
about the point (-5,0). - A rotation by
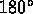 about the point (4,0).
about the point (4,0). - A reflection across the line x=10.
- A reflection across the line x=-7.
- A glide reflection involving a translation to the right by 6
units.
- A glide reflection involving a translation to the left by 8
units.
- Identify the following strip symmetries:
- f(x,y)=(x,y). The identity: I.
- f(x,y)=(-x,y). Reflection about the vertical line x=0:
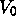 .
. - f(x,y)=(x,-y).
- f(x,y)=(-x,-y).
- f(x,y)=(x+1,y).
- f(x,y)=(x-2,y).
- f(x,y)=(-x+1,y).
- f(x,y)=(-x-2,y).
- f(x,y)=(x+1,-y).
- f(x,y)=(x-2,-y).
- f(x,y)=(-x+1,-y).
- f(x,y)=(-x-2,-y).
- In the next set of exercise,
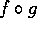 means first perform g,
then perform f. For the following, determine the formula, and then
identify the symmetry:
means first perform g,
then perform f. For the following, determine the formula, and then
identify the symmetry:
-
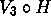 .
. -
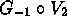 .
. -
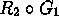 .
. -
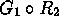 .
. -
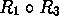 .
. -
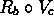 .
. -
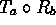 .
. -
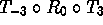 . Explain why this makes sense in a
sentence or two.
. Explain why this makes sense in a
sentence or two. -
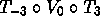 . Explain why this makes sense in a
sentence or two.
. Explain why this makes sense in a
sentence or two. - Find f such that
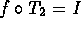 .
. - Find f such that
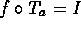 .
. - Find f such that
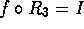 .
. - Find f such that
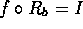 .
. - Find f such that
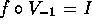 .
. - Find f such that
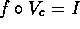 .
. - Find f such that
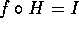 .
. - Find f such that
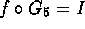 .
. - Find f such that
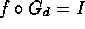 .
.
- Fill in the following composition table, filling in each entry
with
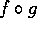 and identifying what kinds of symmetries can result.
(You may have to redraw this chart to make it larger.)
and identifying what kinds of symmetries can result.
(You may have to redraw this chart to make it larger.)

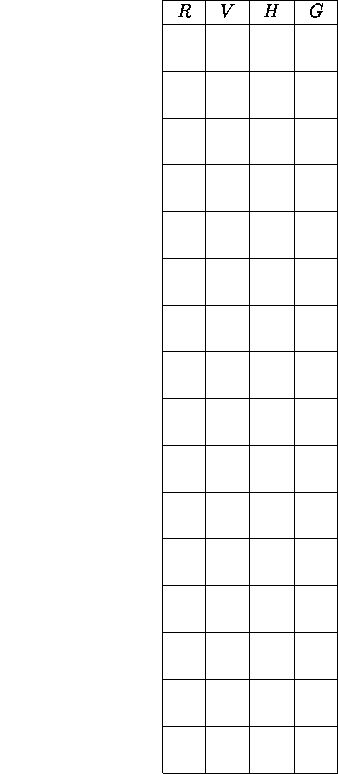
- We will now try to classify repeating strip patterns by the types of
symmetries they have. In the following table, R indicates the
presence of some
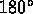 rotational symmetry about a point on the
x-axis, V indicates the presence of a reflectional symmetry across some
vertical line, H in indicates the presence of a reflectional
symmetry across
the x-axis, and G indicates the presence of some nontrivial glide
reflectional symmetry across the x-axis (i.e., where the accompanying
translation is by a non-zero amount, so it is not merely a horizontal
reflection.) For a given row there are sixteen possible ways to
place either a check mark or an x in each cell of the row (why?).
Fill in the table with the sixteen possibilities. For each
possibility, either draw a repeating strip pattern to the right of the
row exhibiting precisely that
combination of symmetries, or else use the results of the
previous chart to briefly
explain why that particular combination of of symmetries is
impossible for any repeating strip pattern. For example, the presence
of H and T (all patterns have T) forces the presence of G, and
the presence of R and V forces the presence of either H or G or both.
rotational symmetry about a point on the
x-axis, V indicates the presence of a reflectional symmetry across some
vertical line, H in indicates the presence of a reflectional
symmetry across
the x-axis, and G indicates the presence of some nontrivial glide
reflectional symmetry across the x-axis (i.e., where the accompanying
translation is by a non-zero amount, so it is not merely a horizontal
reflection.) For a given row there are sixteen possible ways to
place either a check mark or an x in each cell of the row (why?).
Fill in the table with the sixteen possibilities. For each
possibility, either draw a repeating strip pattern to the right of the
row exhibiting precisely that
combination of symmetries, or else use the results of the
previous chart to briefly
explain why that particular combination of of symmetries is
impossible for any repeating strip pattern. For example, the presence
of H and T (all patterns have T) forces the presence of G, and
the presence of R and V forces the presence of either H or G or both.
- Refer to the handout labeled ``Transparency 4'' for samples of
the possible repeating strip patterns. Confirm that you have found
the same number of patterns, and label the patterns you drew according
to the scheme on the handout.



Next: About this document
Up: PolygonsPatterns, and Polyhedra
Previous: Explorations with Clusters and
Carl Lee
Wed Nov 4 12:13:22 EST 1998
![]() is a
function
is a
function ![]() such that for any two points
p and q in the plane, the distance between f(p) and f(q) equals the
distance between p and q. We will (I hope) prove that besides the
identity map f(p)=p, there are only four different types of rigid
motions: translations, rotations about points, reflections across
lines, and glide reflections (a reflection across a line followed by a
translation parallel to the line). Notice that a translation by a
distance of 0 is the identity map, as is a rotation by an angle that is
an integer multiple of
such that for any two points
p and q in the plane, the distance between f(p) and f(q) equals the
distance between p and q. We will (I hope) prove that besides the
identity map f(p)=p, there are only four different types of rigid
motions: translations, rotations about points, reflections across
lines, and glide reflections (a reflection across a line followed by a
translation parallel to the line). Notice that a translation by a
distance of 0 is the identity map, as is a rotation by an angle that is
an integer multiple of ![]() . Also a glide reflection involving a
translation by a distance of 0 is simply a reflection.
. Also a glide reflection involving a
translation by a distance of 0 is simply a reflection.
![]() such that f(S)=S. This doesn't mean that every
point of the subset is fixed by f, but that
such that f(S)=S. This doesn't mean that every
point of the subset is fixed by f, but that ![]() ;
i.e., every point in S is mapped to a point in S, and every point
in S is the image of some point in S.
;
i.e., every point in S is mapped to a point in S, and every point
in S is the image of some point in S.
![]() . We will call
this a strip. What are the possible symmetries of the strip?
. We will call
this a strip. What are the possible symmetries of the strip?

