


Next: Sequence Limits
Up: Elementary Analysis
Previous: Elementary Analysis
- In the following, let S be a subset of the real numbers and
B be a real number. Rewrite each statement symbolically using
quantifiers.
- Definition:
B is an upper bound for S if
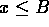 for all
for all 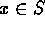 .
. - Definition:
B is the least upper bound for S if B is an upper
bound for S and if B' is any upper bound for S, then
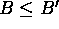 .
. - Definition:
B is a lower bound for S if
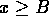 for all
for all 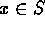 .
. - Definition:
B is the greatest lower bound for S if B is a lower
bound for S and if B' is any lower bound for S, then
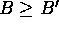 .
. - Definition:
B is a bound for S if
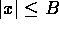 for all
for all 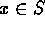 .
. - Definition:
S is a bounded set if it has a bound.
- Least Upper Bound Axiom for the Real Numbers: If S is
nonempty and has an upper bound, then it has a least upper bound.
- Express the following statements symbolically.
- B is not an upper bound for S.
- S has no upper bound.
- B is not a least upper bound for S.
- Prove or disprove.
- The empty set has an upper bound.
- The empty set has a least upper bound.
- If S is a nonempty subset of the real numbers and
S has a lower bound, then it has a greatest lower bound.
- If S is a nonempty subset of the rational
numbers that has an upper bound, then it has a rational least upper
bound.
- The number 3 is an upper bound for the
set
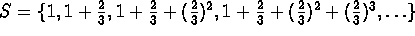 .
. - The number 3 is an upper bound for the set
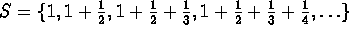 .
. - The set
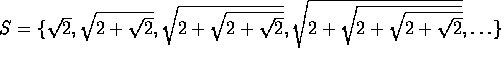 has an upper bound.
has an upper bound. - The set
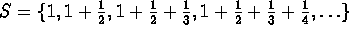 has an upper bound.
has an upper bound.
Carl Lee
Wed Dec 2 12:11:38 EST 1998
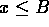 for all
for all 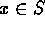 .
.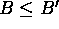 .
.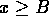 for all
for all 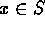 .
.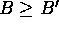 .
.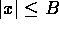 for all
for all 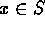 .
.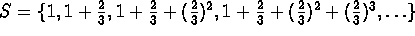 .
.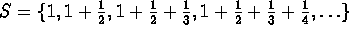 .
.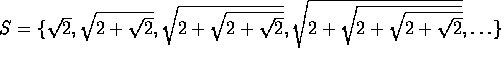 has an upper bound.
has an upper bound.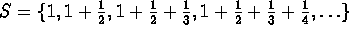 has an upper bound.
has an upper bound.