


Next: About this document
Up: Elementary Analysis
Previous: Boundedness
- In the following, let
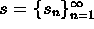 (or
(or
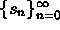 ) be a sequence of real numbers and L is a
real number.
Rewrite each statement symbolically using quantifiers.
) be a sequence of real numbers and L is a
real number.
Rewrite each statement symbolically using quantifiers.
- Definition: The sequence s is said to converge
to L provided that if
 then there is a number N such
that n>N implies that
then there is a number N such
that n>N implies that 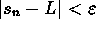 . In this case, s is
called a convergent sequence, L is its limit, and we
write
. In this case, s is
called a convergent sequence, L is its limit, and we
write 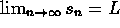 .
. - Definition: The sequence s is said to converge
if it converges to some number L.
- For each of the following sequences, prove whether or not it
converges.
-
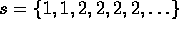 .
. -
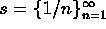 .
. -
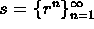 .
. -
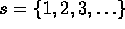 .
. -
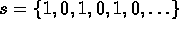 .
. -
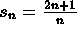 .
. -
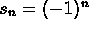 .
. -
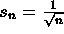 .
. -
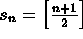 where [x] denotes the
greatest integer not exceeding x.
where [x] denotes the
greatest integer not exceeding x. -
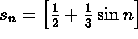 , where [x] is as in
the previous problem.
, where [x] is as in
the previous problem. -
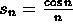 .
. -
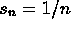 if n is odd and
if n is odd and 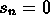 if n is even.
if n is even. -
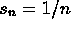 if n is odd and
if n is odd and 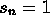 if n is odd.
if n is odd. -
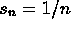 if n is odd and
if n is odd and 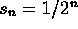 if n is even.
if n is even.
- Prove.
- If s is a convergent sequence, then s is bounded.
- If s is a convergent sequence, then its limit is unique.
- If s and t are sequences such that
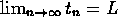 and for every n,
and for every n, 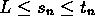 , then
, then 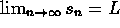 .
. - If
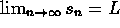 and for every n,
and for every n, 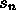 is
in the interval [a,b], then L is also in [a,b].
is
in the interval [a,b], then L is also in [a,b]. - If s is a sequence and L is a number, then
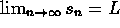 if and only if
if and only if
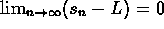 .
. - If s is a bounded sequence and t is a null sequence (a
sequence converging to 0), then st is a null sequence.
- If t is a convergent sequence whose limit is not zero, and for
n in
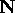 ,
, 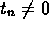 , then 1/t is a bounded sequence.
, then 1/t is a bounded sequence. - Suppose each of s and t is a convergent sequence and c is
a number; then s+t, s-t, and cs are convergent. Also, if
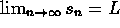 and
and 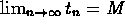 ,
then
,
then 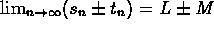 and
and
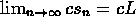 .
. - Suppose each of s and t is a convergent sequence, say
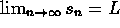 and
and 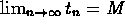 ;
then st is convergent and
;
then st is convergent and 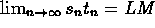 . If,
in addition,
. If,
in addition, 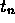 is never 0 and
is never 0 and 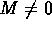 , then s/t is
convergent and
, then s/t is
convergent and 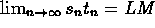 .
.



Next: About this document
Up: Elementary Analysis
Previous: Boundedness
Carl Lee
Wed Dec 2 12:11:38 EST 1998
 then there is a number N such
that n>N implies that
then there is a number N such
that n>N implies that 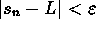 . In this case, s is
called a convergent sequence, L is its limit, and we
write
. In this case, s is
called a convergent sequence, L is its limit, and we
write 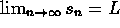 .
.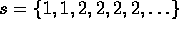 .
.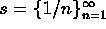 .
.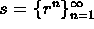 .
.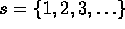 .
.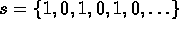 .
.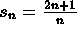 .
.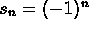 .
.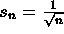 .
.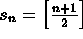 where [x] denotes the
greatest integer not exceeding x.
where [x] denotes the
greatest integer not exceeding x.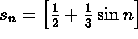 , where [x] is as in
the previous problem.
, where [x] is as in
the previous problem.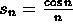 .
.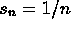 if n is odd and
if n is odd and 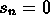 if n is even.
if n is even.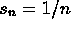 if n is odd and
if n is odd and 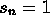 if n is odd.
if n is odd.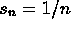 if n is odd and
if n is odd and 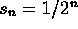 if n is even.
if n is even.
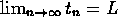 and for every n,
and for every n, 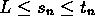 , then
, then 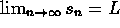 .
.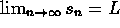 and for every n,
and for every n, 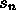 is
in the interval [a,b], then L is also in [a,b].
is
in the interval [a,b], then L is also in [a,b].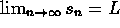 if and only if
if and only if
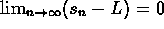 .
.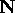 ,
, 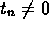 , then 1/t is a bounded sequence.
, then 1/t is a bounded sequence.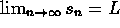 and
and 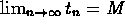 ,
then
,
then 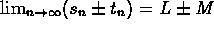 and
and
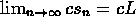 .
.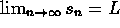 and
and 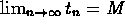 ;
then st is convergent and
;
then st is convergent and 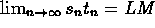 . If,
in addition,
. If,
in addition, 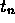 is never 0 and
is never 0 and 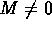 , then s/t is
convergent and
, then s/t is
convergent and 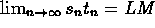 .
.