Classification of Parallels

We have defined two types of parallel lines--hyperparallel and horoparallel. Are these the only types of parallel lines in hyperbolic geometry? Are there lines that are both hyperparallel and limiting parallel? These are the questions that we wish to answer in this section.

Theorem 13.12:  Let be the limiting parallel ray to through P and let Q and X' be the feet of P and X, respectively, in . Then PQ>XX'.

Proof: If then by Theorem 14.5. Thus, is the angle of parallelism for X and . Thus, it is acute. Therefore, is obtuse. This implies that and therefore PQ>XX'.

This shows that the distance form X to decreases as the distance from P to X increases along the limiting parallel ray. In fact, one can show that the distance from X to approaches 0. Note that we have seen that for hyperparallel lines the further one gets from the common perpendicular, the greater the distance between the lines. This gives one the impression that these types of parallel lines should be distinct.

Corollary 1: If in a given direction, then and k have no common perpendicular.

Proof: Let so that and assume that there is a point so that

(i)

, and

(ii)

MM' is a common perpendicular to and k.

From Theorem 14.13 PQ>MM'>XX'. By Theorem 14.10 MM'<XX', a contradiction. Thus, and k have no common perpendicular.

This tells us that if two lines are limiting parallel, then they are not hyperparallel. We now need to show that if two lines are non-intersecting and are not limiting parallel, then they must be hyperparallel. Having done this we will then know that there are only two types of parallel lines.

Theorem 13.13:  Given lines m and n so that

1. , and
2. m does not contain a limiting parallel ray to n in either direction.

Then .

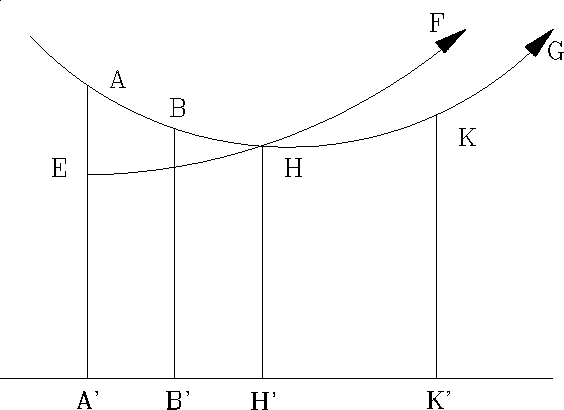
Proof: We need to find two points that are equidistant from m; i.e., . If this is true, then by Theorem 14.11 the perpendicular bisector of HK is the common perpendicular to m and n. By Theorem 14.11 this common perpendicular is unique. It follows then that .

(i) The search for H and K.

Let with feet . If we are done. Assume that these segments are not congruent. Then, we may assume that AA'>BB', since one must be greater than the other. There is a point so that .

There is a unique ray on the same side of as B so that with .

CLAIM: . (Proof will follow.)

Call this point of intersection H. The there is a unique point so that . Then, by SAS . Thus, . We also have that , so that by Angle Subtraction it follows that . Since HH' and KK' are perpendicular to m, we have by Hypotenuse-Angle that . Therefore, , and H and K are equidistant from m.

Thus, we are finished once we have proved the claim.

It turns out that the claim is the hardest item to prove in the whole theorem. It takes us through some strange territory.