Skip to main content\(\newcommand{\N}{\mathbb N}
\newcommand{\Z}{\mathbb Z}
\newcommand{\Q}{\mathbb Q}
\newcommand{\R}{\mathbb R}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\definecolor{fillinmathshade}{gray}{0.9}
\newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}}
\)
Exercises 3.3 Practice Problems
1.
Suppose
\(f(x) = (x+2)^2 \) and
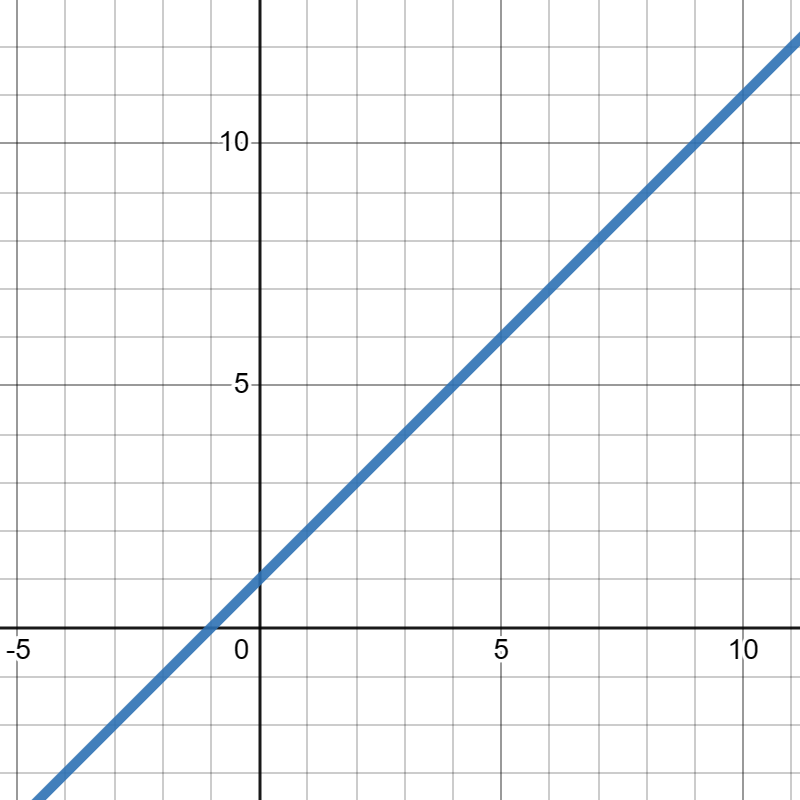
\(g(x)\) is given in the graph below:
Evaluate each of the following:
-
\(\displaystyle f(g(-2))\)
-
\(\displaystyle f(g(4))\)
-
\(\displaystyle g(g(6))\)
-
\(\displaystyle g(f(0))\)
-
\(\displaystyle f(g(0))\)
Answer.
-
\(\displaystyle f(g(-2))=1\)
-
\(\displaystyle f(g(4))=49\)
-
\(\displaystyle g(g(6))=8\)
-
\(\displaystyle g(f(0))=5\)
-
\(\displaystyle f(g(0))=9\)
2.
Suppose
\(f(x) = \frac{1}{2}x \) and
\(g(x)\) is given in the table below:
Table 3.3.1.
| \(x\) |
\(-1\) |
\(1\) |
\(2\) |
\(5\) |
\(4\) |
| \(g(x)\) |
\(0\) |
\(2\) |
\(4\) |
\(1\) |
\(0\) |
Evaluate each of the following:
-
\(\displaystyle f(g(-1))\)
-
\(\displaystyle f(g(5))\)
-
\(\displaystyle g(g(2))\)
-
\(\displaystyle g(f(-2))\)
-
\(\displaystyle f(g(1))\)
Answer.
-
\(\displaystyle f(g(-1))=0\)
-
\(\displaystyle f(g(5))=\frac{1}{2}\)
-
\(\displaystyle g(g(2))=0\)
-
\(\displaystyle g(f(-2))=0\)
-
\(\displaystyle f(g(1))=1\)
3.
Suppose
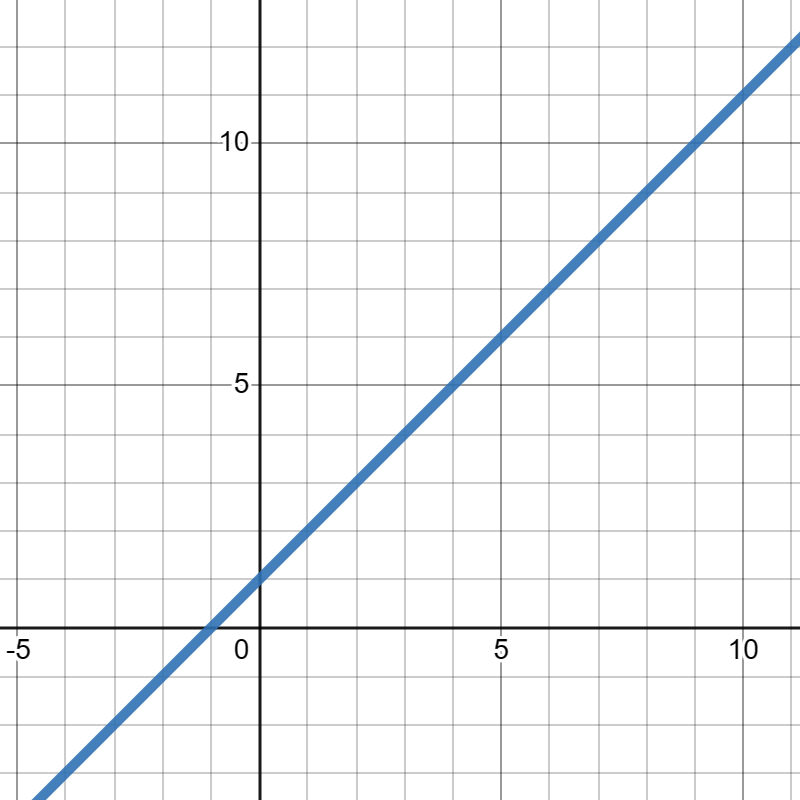
\(f(x)\) is given in the graph below and
\(g(x)\) is given in the table below:
Table 3.3.2.
| \(x\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
| \(g(x)\) |
\(0\) |
\(2\) |
\(4\) |
\(1\) |
\(5\) |
Evaluate each of the following or, if there is insufficient information given to answer the question, state that.
-
\(\displaystyle f(g(1))\)
-
\(\displaystyle f(g(5))\)
-
\(\displaystyle g(g(2))\)
-
\(\displaystyle g(f(-2))\)
-
\(\displaystyle f(g(1))\)
Answer.
-
\(\displaystyle f(g(1))=5\)
-
\(\displaystyle f(g(5))=0\)
-
\(\displaystyle g(g(2))=2\)
-
There is insuffient information given to compute.
-
\(\displaystyle f(g(3))=1\)
4.
Suppose
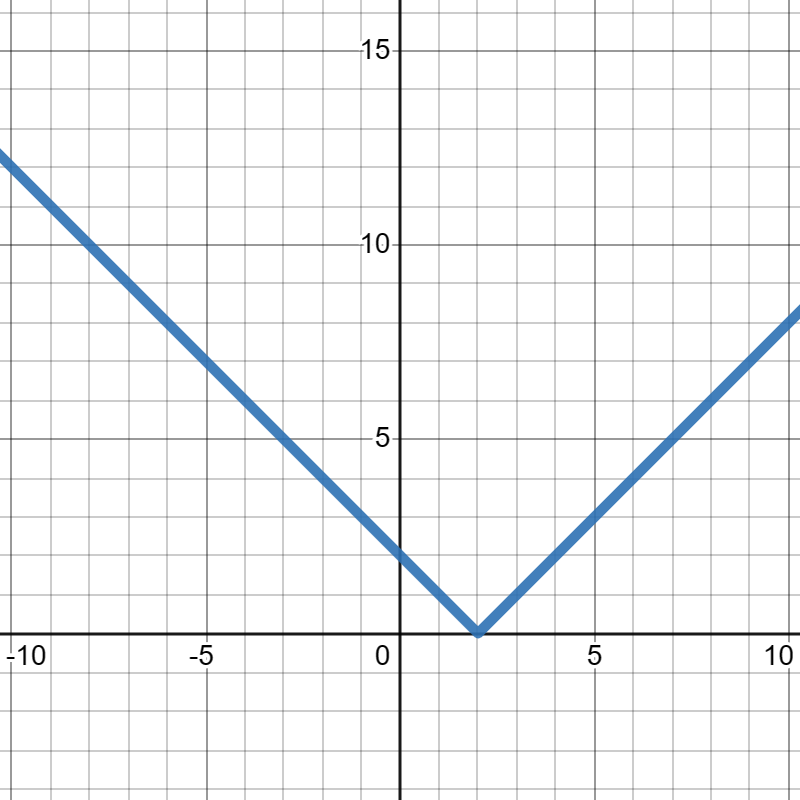
\(g(x)\) is given in the graph below and
\(h(x)\) is given in the table below:
Table 3.3.3.
| \(x\) |
\(0\) |
\(2\) |
\(4\) |
\(6\) |
\(8\) |
| \(h(x)\) |
\(0\) |
\(8\) |
\(4\) |
\(6\) |
\(2\) |
Evaluate each of the following or, if there is insufficient information given to answer the question, state that.
-
\(\displaystyle h(g(1))\)
-
\(\displaystyle h(g(4))\)
-
\(\displaystyle h(g(2))\)
-
\(\displaystyle g(h(2))\)
-
\(\displaystyle h(h(2))\)
Answer.
-
There is insuffient information given to compute.
-
\(\displaystyle h(g(4))=8\)
-
\(\displaystyle h(g(2))=0\)
-
\(\displaystyle g(h(2))=0\)
-
\(\displaystyle h(h(2))=2\)
5.
Suppose
\(g(x)=x^2\) and
\(h(x)=|x+1|\) is given in the table below:
Evaluate each of the following or, if there is insufficient information given to answer the question, state that.
-
\(\displaystyle h(g(1))\)
-
\(\displaystyle h(g(2))\)
-
\(\displaystyle h(g(-1))\)
-
\(\displaystyle g(h(-1))\)
-
\(\displaystyle h(h(-1))\)
Answer.
-
\(\displaystyle h(g(1))=2\)
-
\(\displaystyle h(g(2))=5\)
-
\(\displaystyle h(g(-1))=2\)
-
\(\displaystyle g(h(-1))=0\)
-
\(\displaystyle h(h(-1))=1\)
6.
Suppose \(f(x)=2x+3\) and \(g(x)=x^2+x-1\text{.}\) Find each of the following. You do NOT need to simplify.
-
\(\displaystyle f(g(x))\)
-
\(\displaystyle g(f(x))\)
-
\(\displaystyle f(f(x))\)
-
\(\displaystyle g(g(x))\)
Answer.
-
\(\displaystyle f(g(x))=2(x^2+x-1)+3\)
-
\(\displaystyle g(f(x))=(2x+3)^2+(2x+3)-1\)
-
\(\displaystyle f(f(x))=2(2x+3)+3\)
-
\(\displaystyle g(g(x))=(x^2+x-1)^2+(x^2+x-1)-1\)
7.
Suppose \(f(x)=|x+3|\) and \(g(x)=3x-1\text{.}\) Find each of the following. You do NOT need to simplify.
-
\(\displaystyle f(g(x))\)
-
\(\displaystyle g(f(x))\)
-
\(\displaystyle f(f(x))\)
-
\(\displaystyle g(g(x))\)
Answer.
-
\(\displaystyle f(g(x))=|(3x-1)+3|\)
-
\(\displaystyle g(f(x))=3|x+3|-1\)
-
\(\displaystyle f(f(x))=||x+3|+3|\)
-
\(\displaystyle g(g(x))=3(3x-1)-1\)
8.
Suppose \(f(x)=\frac{1}{2}x+1\) and \(g(x)=\frac{x+1}{2}\text{.}\) Find each of the following. You do NOT need to simplify.
-
\(\displaystyle f(g(x))\)
-
\(\displaystyle g(f(x))\)
-
\(\displaystyle f(f(x))\)
-
\(\displaystyle g(g(x))\)
Answer.
-
\(\displaystyle f(g(x))=\frac{1}{2}\left(\frac{x+1}{2}\right)+1\)
-
\(\displaystyle g(f(x))=\frac{\left(\frac{1}{2}x+1\right)+1}{2}\)
-
\(\displaystyle f(f(x))=\frac{1}{2}\left(\frac{1}{2}x+1\right)+1\)
-
\(\displaystyle g(g(x))=\frac{\left(\frac{x+1}{2}\right)+1}{2}\)
9.
Suppose \(f(x)=\sqrt{x}\) and \(g(x)=4x+5\text{.}\) Find each of the following. You do NOT need to simplify.
-
\(\displaystyle f(g(x))\)
-
\(\displaystyle g(f(x))\)
-
\(\displaystyle f(f(x))\)
-
\(\displaystyle g(g(x))\)
Answer.
-
\(\displaystyle f(g(x))=\sqrt{4x+5}\)
-
\(\displaystyle g(f(x))=4\sqrt{x}+5\)
-
\(\displaystyle f(f(x))=\sqrt{\sqrt{x}}\)
-
\(\displaystyle g(g(x))=4(4x+5)+5\)