1.
\(f(x)=3-8x\)
Exercises 2.6 Practice Problems
Exercise Group.
2.
\(f(x)=6x-4\)
3.
\(f(x)=26\)
4.
\(f(x)=-x+6\)
5.
\(f(x)=2x\)
6.
\(f(x)=-\left(\frac{2}{3}\right)x + 1\)
Exercise Group.
7.
\(g(x)=2-4x\)
8.
\(f(x)=3x-3\)
9.
\(g(x)=12\)
10.
\(g(x)=x-1\)
11.
\(g(x)=x\)
12.
\(g(x)=-\frac{1}{4}x + 2\)
Exercise Group.
13.
Evaluate all four of the above functions given \(x=1 \text{.}\)
14.
Evaluate all four of the above functions given \(x=a \text{.}\)
15.
Evaluate all four of the above functions given \(x=0 \text{.}\)
16.
Evaluate all four of the above functions given \(x=2z \text{.}\)
17.
Evaluate all four of the above functions given \(x=\frac{1}{2} \text{.}\)
18.
Evaluate all four of the above functions given \(x=b+5 \text{.}\)
19.
Suppose \(a(t)= \frac{1}{19}\text{.}\)
-
Evaluate \(a(1)\text{.}\)
-
Evaluate \(a(b+c)\text{.}\)
-
Evaluate \(a(9)\text{.}\)
-
Evaluate \(a(\frac{1}{19})\text{.}\)
20.
Suppose \(d(t)=\pi t\text{.}\)
-
Evaluate \(d(0)\text{.}\)
-
Evaluate \(d(a+h)\text{.}\)
-
Evaluate \(d(x)\text{.}\)
-
Evaluate \(d(\sqrt{x+3})\text{.}\)
21.
Suppose
\begin{equation*}
g(x) = \begin{cases}\sqrt{x} \amp x \gt 2 \\ x^2 \amp -3 \lt x \le 2 \\ x+3 \amp x \le -3 \end{cases}
\end{equation*}
We want to evaluate each of the following:
-
\(\displaystyle g(0)\)
-
\(\displaystyle g(-5)\)
-
\(\displaystyle g(10)\)
-
\(\displaystyle g(2)\)
22.
Suppose
\begin{equation*}
h(t) = \begin{cases}\frac{1}{2}t \amp t \ge 3 \\ t^3 \amp 0 \lt t \lt 3 \\ t+3 \amp t \le 0 \end{cases}
\end{equation*}
We want to evaluate each of the following:
-
\(\displaystyle h(1)\)
-
\(\displaystyle h(3)\)
-
\(\displaystyle h(0)\)
-
\(\displaystyle h(-3)\)
23.
Suppose
\begin{equation*}
f(t) = \begin{cases}\frac{1}{3}t \amp t \ge 5 \\ \sqrt{t} \amp 1 \lt t \lt 5 \\ t \amp t \le 1 \end{cases}
\end{equation*}
We want to evaluate each of the following:
-
\(\displaystyle f(1)\)
-
\(\displaystyle f(5)\)
-
\(\displaystyle f(0)\)
-
\(\displaystyle f\left(\frac{3}{2}\right)\)
24.
Suppose
\begin{equation*}
f(x) = \begin{cases}\frac{1}{x} \amp x \gt 0 \\ x \amp x=0 \\ -\frac{1}{x} \amp x \lt 0 \end{cases}
\end{equation*}
We want to evaluate each of the following:
-
\(\displaystyle f(-1)\)
-
\(\displaystyle f(0)\)
-
\(\displaystyle f(2)\)
-
\(\displaystyle f\left(\frac{1}{2}\right)\)
25.
Suppose
\begin{equation*}
f(x) = \begin{cases}\frac{1}{2} \amp x \gt 10 \\ 2x \amp x=10 \\ -1 \amp x \lt 10 \end{cases}
\end{equation*}
We want to evaluate each of the following:
-
\(\displaystyle f(-10)\)
-
\(\displaystyle f(0)\)
-
\(\displaystyle f(10)\)
-
\(\displaystyle f(20)\)
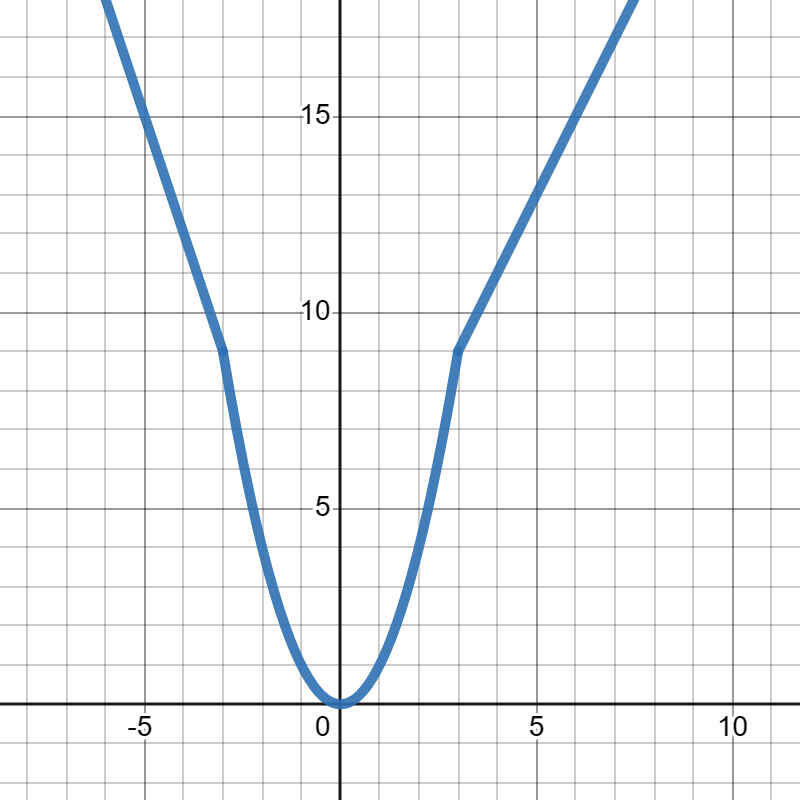
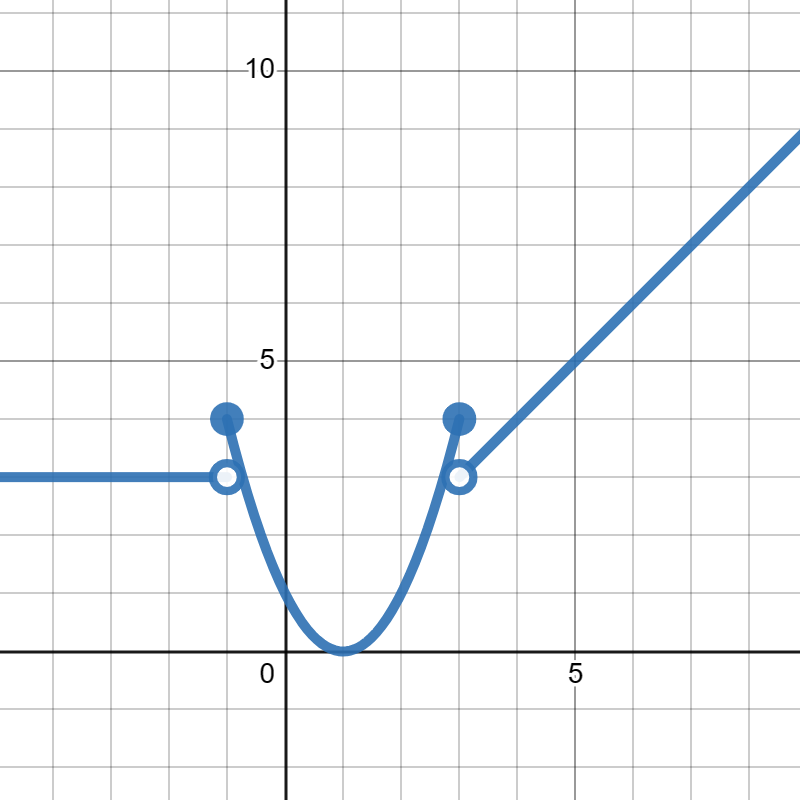
26.
Suppose \(g(x)\) is given in the graph below:
Evaluate each of the following:
-
\(\displaystyle g(-2)\)
-
\(\displaystyle g(4)\)
-
\(\displaystyle g(6)\)
-
\(\displaystyle g(8)\)
-
\(\displaystyle g(9)\)
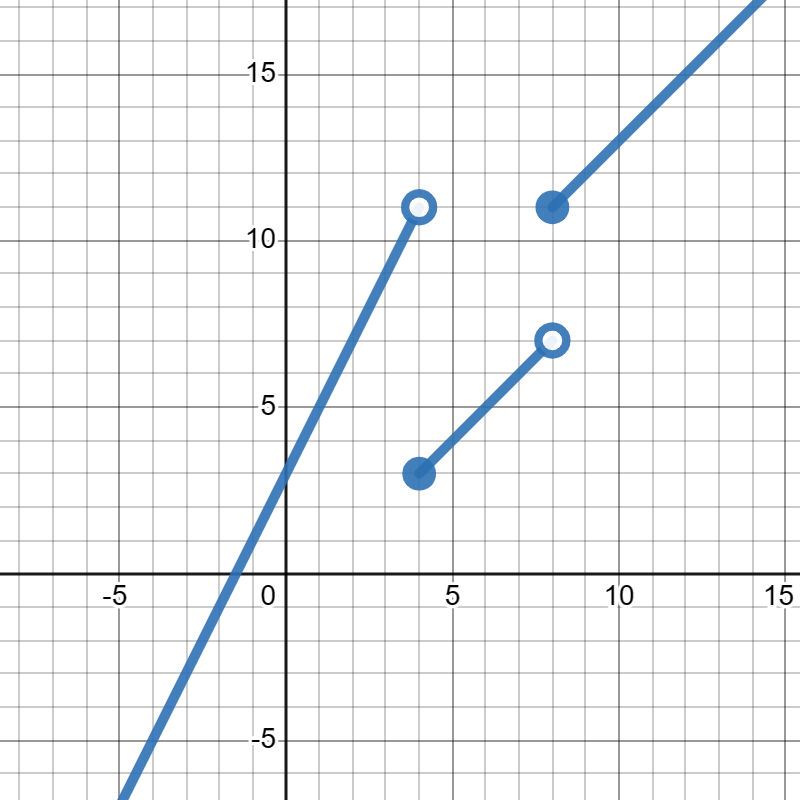
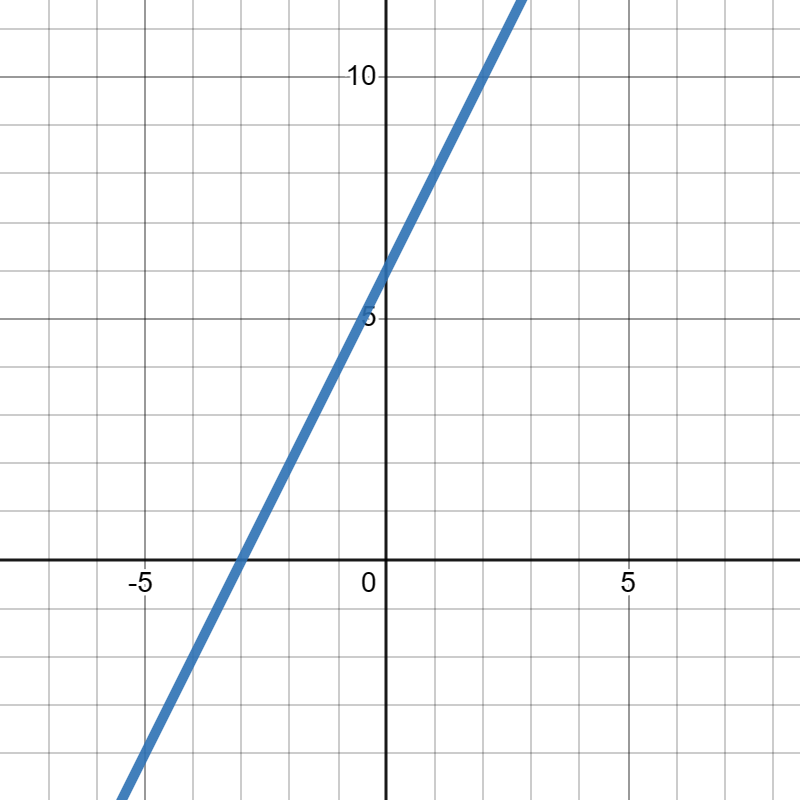
27.
Suppose \(f(x)\) is given in the graph below:
Evaluate each of the following:
-
\(\displaystyle f(-3)\)
-
\(\displaystyle f(0)\)
-
\(\displaystyle f(3)\)
-
\(\displaystyle f(5)\)
-
\(\displaystyle f(7)\)
28.
Suppose \(f(x)\) is given in the table below:
| \(x\) | \(f(x)\) |
| \(-3\) | \(1\) |
| \(0\) | \(2\) |
| \(3\) | \(-7\) |
| \(6\) | \(/pi\) |
| \(\frac{1}{3}\) | \(4.31\) |
Evaluate each of the following:
-
\(\displaystyle f(-3)\)
-
\(\displaystyle f(0)\)
-
\(\displaystyle f(3)\)
-
\(\displaystyle f(6)\)
-
\(\displaystyle f(\frac{1}{3})\)
29.
Suppose \(f(t)\) is given in the table below:
| \(t\) | \(f(t)\) |
| \(0\) | \(1\) |
| \(1\) | \(2\) |
| \(2\) | \(3\) |
| \(3\) | \(4\) |
| \(4\) | \(5\) |
Evaluate each of the following:
-
\(\displaystyle f(0)\)
-
\(\displaystyle f(1)\)
-
\(\displaystyle f(2)\)
-
\(\displaystyle f(3)\)
-
\(\displaystyle f(4)\)
30.
| x | f(x) | g(x) | h(x) |
| 0 | 9 | 4 | 1 |
| 1 | -2 | 5.5 | -3 |
| 2 | 6 | 6 | 6 |
| 3 | 7 | 0 | 8 |
| 4 | -1 | 8 | -4 |
Evaluate each of the following:
-
\(\displaystyle h(0)\)
-
\(\displaystyle f(1)\)
-
\(\displaystyle g(2)\)
-
\(\displaystyle f(3)\)
-
\(\displaystyle h(4)\)
31.
Suppose \(m(x)\) is given in the table below:
| x | 1 | 3 | 5 | 7 | 9 |
| m(x) | 6 | 2 | -1 | -5 | -8 |
Evaluate each of the following:
-
\(\displaystyle m(5)\)
-
\(\displaystyle m(1)\)
-
\(\displaystyle m(9)\)
-
\(\displaystyle m(3)\)
-
\(\displaystyle m(7)\)
Exercise Group.
32.
Evaluate \(2f(2)-g(0)+1\text{.}\)
33.
Evaluate \(g(2)-(g(-2))^2\text{.}\)
34.
Evaluate \(5g(-1)+4f(3)\text{.}\)
35.
Evaluate \(\frac{1}{2}f(5)-2f(0)\text{.}\)
36.
Evaluate \((f(-2))^2-f(0)-(g(2))^3\text{.}\)
Exercise Group.
| x | 1 | 2 | 3 | 4 | 5 |
| g(x) | 6 | 4 | -1 | 7 | 0 |
37.
Evaluate \(2f(2)-g(1)+1\text{.}\)
38.
Evaluate \(g(4)-(g(3))^3\text{.}\)
39.
Evaluate \(2g(1)-3f(5)\text{.}\)
40.
Evaluate \(\frac{1}{2}f(10)-3f(1)\text{.}\)
41.
Evaluate \((f(-2))^2-g(2)-\frac{1}{3}g(5)\text{.}\)
Exercise Group.
| x | 0 | 2 | 4 | 6 | 8 |
| h(x) | 2 | 3 | 9 | 1 | 4 |
42.
Evaluate \(4h(2)-g(0)+3\text{.}\)
43.
Evaluate \(g(4)-\frac{1}{2}(h(6))^3\text{.}\)
44.
Evaluate \(2g(1)+4h(8)\text{.}\)
45.
Evaluate \(\frac{1}{2}g(10)-3h(0)\text{.}\)
46.
Evaluate \((h(4))^2-6g(2)-\frac{1}{3}g(1)\text{.}\)
Exercise Group.
| \(x\) | \(f(x)\) |
| \(0\) | \(2\) |
| \(1\) | \(4\) |
| \(2\) | \(6\) |
| \(3\) | \(8\) |
| \(4\) | \(10\) |
47.
Evaluate \(3f(2)-g(2)+3\text{.}\)
48.
Evaluate \(g(10)-\frac{1}{4}(f(3))^2\text{.}\)
49.
Evaluate \(3g(1)+4f(4)\text{.}\)
50.
Evaluate \(\frac{1}{5}g(6)-3f(0)\text{.}\)
51.
Evaluate \((f(1))^2-2g(2)-\frac{1}{3}g(-4)\text{.}\)
Exercise Group.
Suppose \(f(x)= 4x-8\text{.}\)
52.
Solve \(f(x)=0\text{.}\)
53.
Evaluate \(f(0)\text{.}\)
54.
Evaluate \(f(2)\text{.}\)
55.
Solve \(f(x)=\frac{1}{2}\text{.}\)
56.
Solve \(f(x)=10\text{.}\)
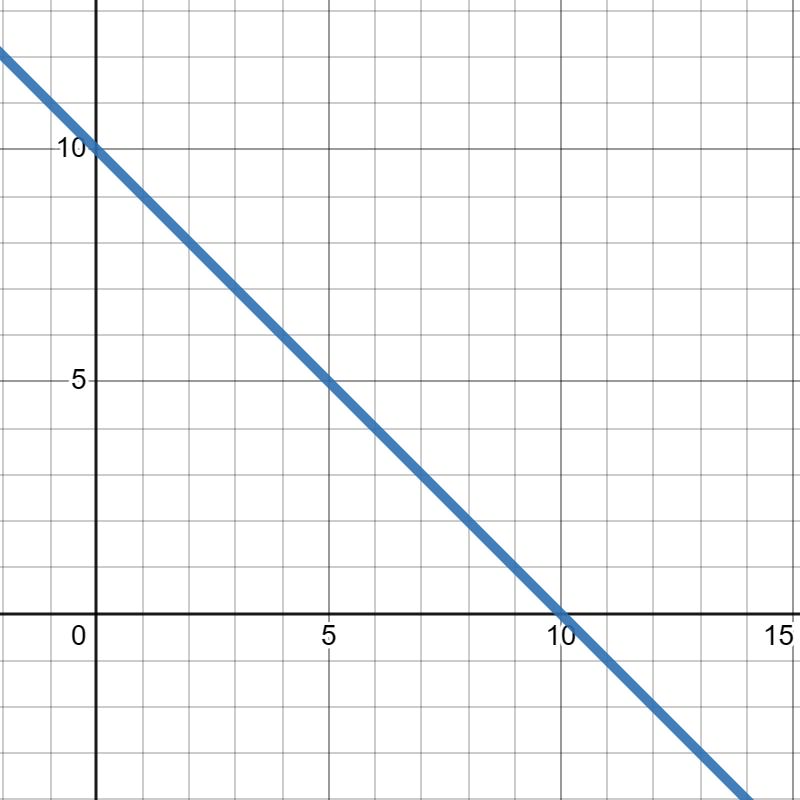
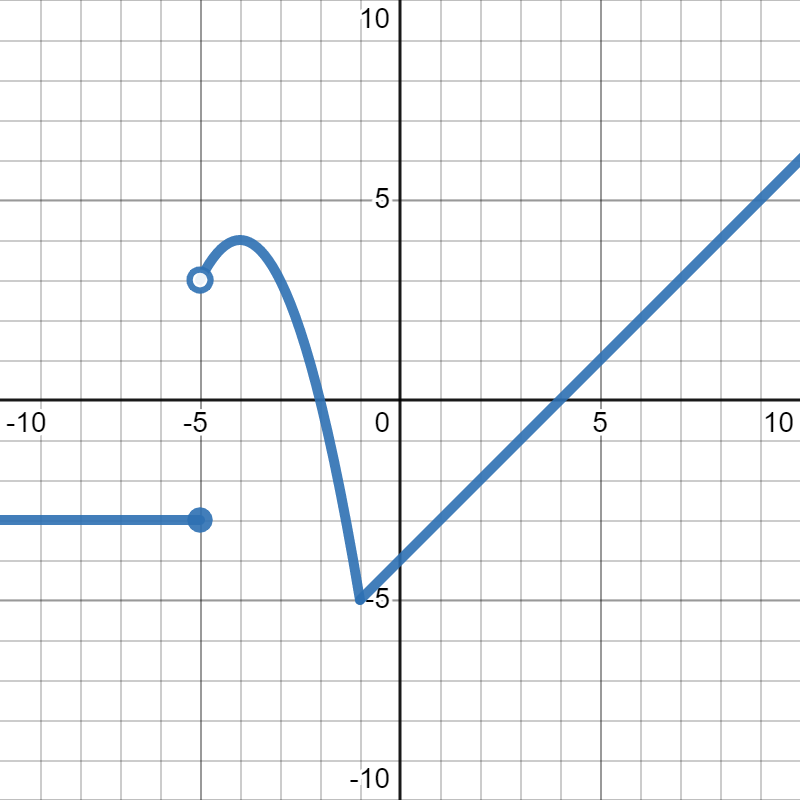
Exercise Group.
Suppose \(g(x)\) is given in the graph below.
57.
Solve \(g(x)=0\text{.}\)
58.
Evaluate \(g(0)\text{.}\)
59.
Evaluate \(g(1)\text{.}\)
60.
Solve \(g(x)=-2\text{.}\)
61.
Solve \(g(x)=4\text{.}\)
Exercise Group.
Suppose \(f(x)\) is given in the table below.
| \(x\) | \(f(x)\) |
| \(1\) | \(3\) |
| \(2\) | \(6\) |
| \(3\) | \(9\) |
| \(4\) | \(12\) |
| \(5\) | \(15\) |
62.
Solve \(f(x)=12\text{.}\)
63.
Evaluate \(f(1)\text{.}\)
64.
Evaluate \(f(3)\text{.}\)
65.
Solve \(f(x)=6\text{.}\)
66.
Solve \(f(x)=9\text{.}\)
Exercise Group.
Suppose \(g(x)\) is given in the graph below.
67.
Solve \(g(x)=1\text{.}\)
68.
Evaluate \(g(-1)\text{.}\)
69.
Evaluate \(g(1)\text{.}\)
70.
Solve \(g(x)=6\text{.}\)
71.
Solve \(g(x)=5\text{.}\)
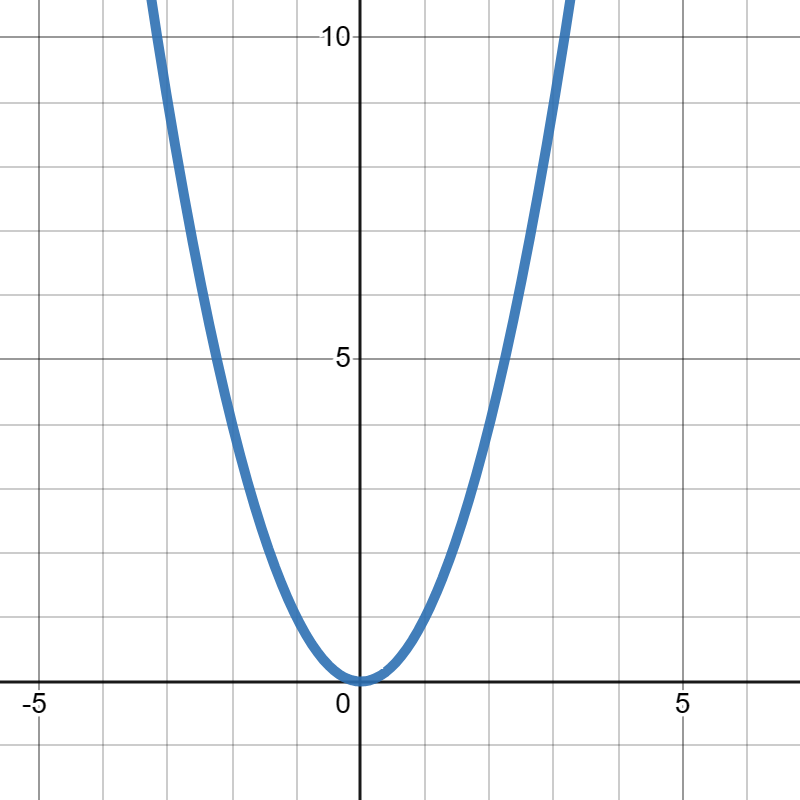
Exercise Group.
Suppose \(g(x)=(x-1)^2\) .
72.
Solve \(g(x)=9\text{.}\)
73.
Evaluate \(g(1)\text{.}\)
74.
Evaluate \(g(2)\text{.}\)
75.
Solve \(g(x)=16\text{.}\)
76.
Solve \(g(x)=0\text{.}\)
