Exercises 5.4 Practice Problems
2.
3.
4.
Compute the slope of the line below.
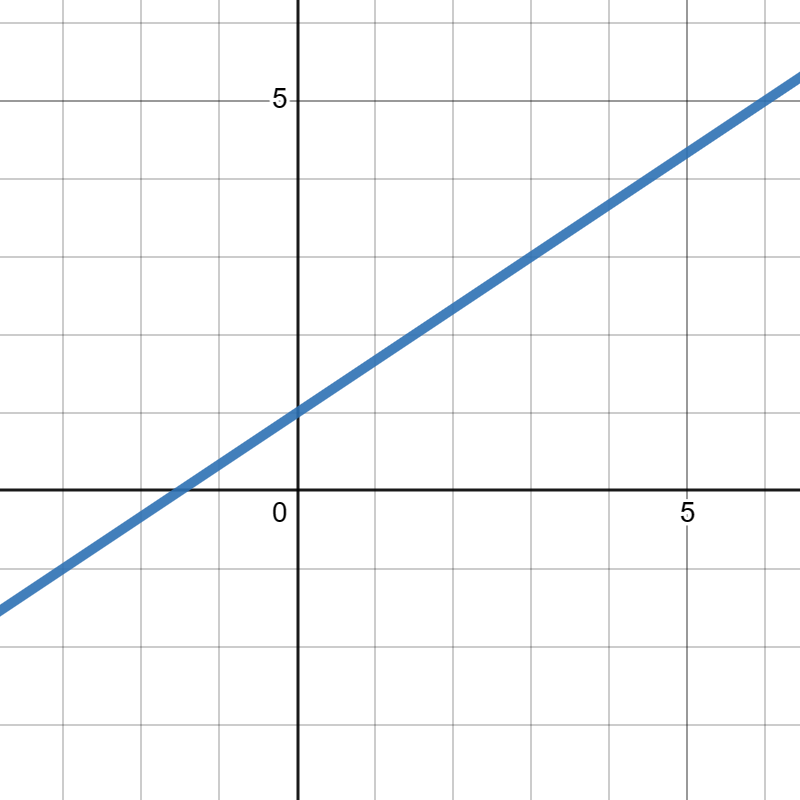
5.
Compute the slope of the line below.
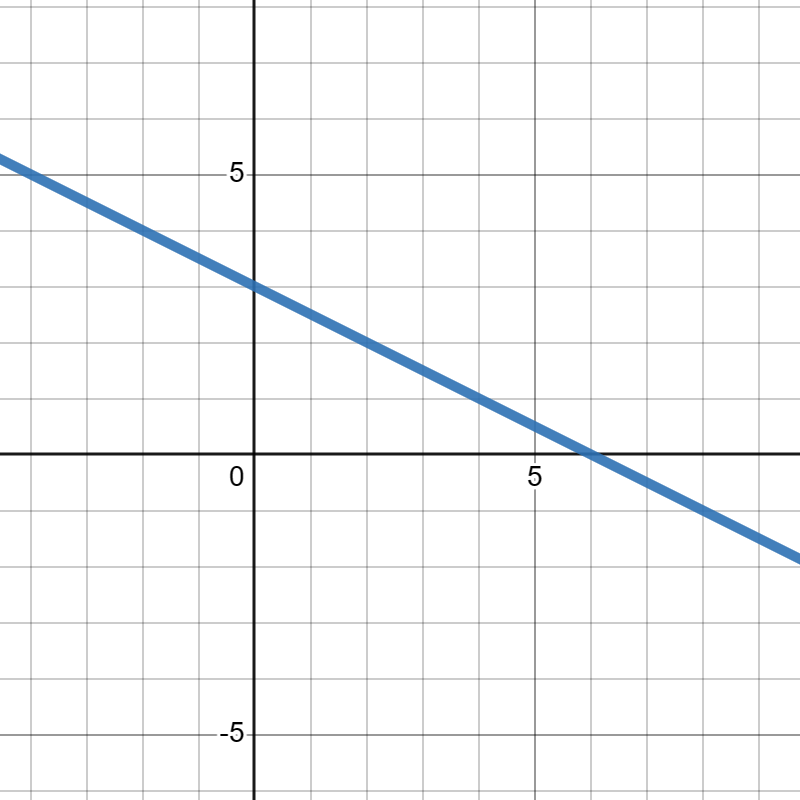
6.
Compute the slope of the line below.
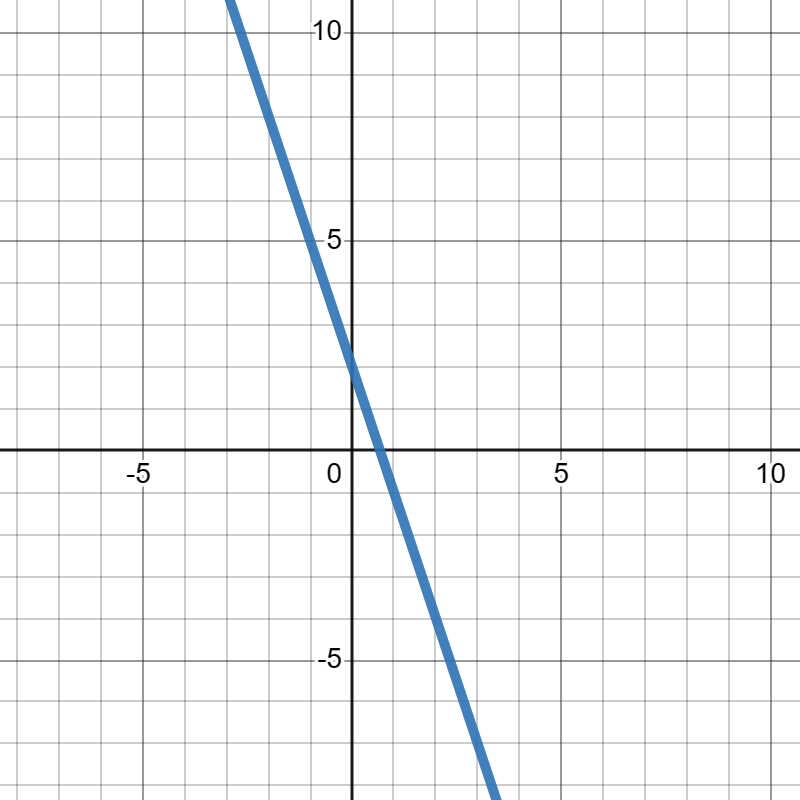
7.
8.
9.
10.
11.
Write the equation of the linear function with slope \(\frac{-1}{2}\) and through the point \((1,-1)\text{.}\)
12.
13.
Write the equation of the linear function that goes through the points \((1,-1)\) and \((3,-5)\text{.}\)
14.
Write the equation of the linear function that goes through the points \((0,0)\) and \((6,2)\text{.}\)
15.
Write the equation of the horizontal line that goes through the point \((1,-3)\text{.}\)
16.
Write the equation of the vertical line that goes through the point \((5,-2)\text{.}\)
17.
Write the equation of the horizontal line that goes through the point \((2,4)\text{.}\)
18.
Write the equation of the vertical line that goes through the point \((2,2)\text{.}\)
19.
Scientists are studying how a snake grows. Based on their measurements, the length of the snake \(t\) years after its hatching is represented by \(l(t)=2t+6\) inches.
-
How much does this snake grow each year, based on this model?
-
How long is the snake when it hatches?
-
Based on this model, how long do you expect the snake to be 5 years after it hatches?
20.
Beauticians are studying how fast a test client’s hair grows in order to decide how often they should schedule a trim. Based on their measurements, the length of the client’s hair \(t\) weeks after their first appointment is represented by \(l(t)=.5t+20\) inches.
-
How much does the client’s hair grow each week, based on this model?
-
How long is the client’s hair at their first appointment?
-
Based on this model, how long do you expect the client’s hair to be 4 weeks after their first appointment?
-
Based on this model, if the client wants to trim their hair once it reaches 24 inches in length, how many weeks after their first appointment should they schedule their next appointment?
21.
Economists are studying the supply and demand of pencil sharpeners among UK freshmen. Their analysis of the data they collected estimates that at a price of \(x\) dollars, the number of pencil sharpeners that will be bought is given by the function \(d(x)=-813x+5020\text{.}\) We want to answer the following questions:
-
As the price increases, what happens to demand (the number of pencil sharpeners purchased)?
-
If they give away the pencil sharpeners for free, how many should they expect students will take?
-
If they sell the pencil sharpeners for $5, how many should they expect students will buy?
22.
Scientists are studying how five town’s populations have changed since 2020. Based on their data, they have created the following equations to model the populations:
| Town | Population |
| Town A | \(10x+491\) |
| Town B | \(21x+134\) |
| Town C | \(-25x+666\) |
| Town D | \(55x+687\) |
| Town E | \(-30x+597\) |
Use the table above to answer the following questions:
-
Which town had the largest population in 2020?
-
Which towns are shrinking?
-
Which town is shrinking the fastest?
23.
Scientists are studying how five college’s enrollment populations have changed since 2020. Based on their data, they have created the following equations to model the populations:
| College | Population |
| College A | \(-100x+49126\) |
| College B | \(2120x+61834\) |
| College C | \(238x+6766\) |
| College D | \(-2955x+81287\) |
| College E | \(301x+54797\) |
Use the table above to answer the following questions:
-
Which college had the smallest population in 2020?
-
Which colleges are growing?
-
Which college is growing the fastest?
