Section 8.4 Domain from a Formula
The theme that you’ll see repeated in this section is that the domain of a function is everything except where there are problems. We’re going to look at two different potential problems in this section: square roots of variables and variables in the denominator of a fraction.
Subsection 8.4.1 Square Roots of Variables
Let’s do a warm-up problem. Suppose \(f(x)=2\sqrt{x+3}+1\text{.}\) We want to find the following values:
-
\(\displaystyle f(0)\)
-
\(\displaystyle f(-1)\)
-
\(\displaystyle f(-3)\)
-
\(\displaystyle f(-5)\)
Remember that for each one, the number given is the input, so we replace the \(x\) in the formula with that number. Let’s do each of them one by one:
-
\(\displaystyle f(0) = 2\sqrt{0+3}+1=2\sqrt{3}+1\)
-
\(\displaystyle f(-1) = 2\sqrt{-1+3}+1=2\sqrt{2}+1\)
-
\(\displaystyle f(-3) = 2\sqrt{-3+3}+1=2\sqrt{0}+1=1\)
-
\(f(-5) = 2\sqrt{-5+3}+1 = 2\sqrt{-2}+1\text{,}\) which is undefined in our class.
Notice that in the last question, we discovered that \(f(-5)\) is undefined because it results in trying to take the square root of a negative number. Remember from Section 8.2 that the domain is all of the possible inputs. Since \(-5\) is not a possible input to this function, that means that \(-5\) is not in the domain of \(f(x)\text{.}\)
Example 8.4.2.
Let’s look at the example from the warm-up. Since the only part that can cause problems is the part under the square root, we can ignore the 1 and the 2. We just need to figure out where \(x+3\) is non-negative. In other words, we set
\begin{equation*}
x+3 \ge 0
\end{equation*}
Subtracting 3 from both sides, we end up with
\begin{equation*}
x \ge -3
\end{equation*}
Now, all that we have to do is turn it into interval notation. You might find it helpful to draw a number line. Our final answer is \([-3,\infty)\text{.}\)
Checkpoint 8.4.3.
Answer.
\(\left(-\infty,\frac{2}{5}\right]\)
Solution.
Since the only part that causes a problem is the part inside the square root, we can ignore the 4 and the 7. All we need to do is set \(5-2x\ge0\) and solve for x. There are two ways you could solve it, depending on what your first step is. We’ll show you both.
If you start by subrtracting 5 from both sides, you’ll need to remember that when you eventually divide by \(-2\text{,}\) you’ll need to flip the direction of the inequality. Here is what that version looks like:
\begin{align*}
5-2x \amp \ge 0\\
-2x \amp \ge -5 \\
x \amp \le \frac{-5}{-2}\\
x \amp \le \frac{5}{2}
\end{align*}
If you start by adding \(2x\) to both sides, you won’t end up dividing by a negative number, but your variable will be on the other side of the equal sign. Here is what that version looks like:
\begin{align*}
5-2x \amp \ge 0\\
5 \amp \ge 2x \\
\frac{5}{2} \amp \ge x
\end{align*}
In either case, our answer is all of the numbers that are less than or equal to \(\frac{5}{2}\text{.}\) In interval notation, our final answer is \(\left(-\infty,\frac{5}{2}\right]\text{.}\)
Subsection 8.4.2 Variables in the Denominator
Let’s do a warm-up problem. Suppose \(f(x)=\dfrac{x+3}{x-1}\text{.}\) We want to find the following values:
-
\(\displaystyle f(0)\)
-
\(\displaystyle f(-1)\)
-
\(\displaystyle f(1)\)
-
\(\displaystyle f(2)\)
Remember that for each one, the number given is the input, so we replace the \(x\) in the formula with that number. Let’s do each of them one by one:
-
\(\displaystyle f(0)=\dfrac{0+3}{0-1} = \dfrac{3}{-1} = -3\)
-
\(\displaystyle f(-1)=\dfrac{-1+3}{-1-1} = \dfrac{2}{-2} = -1\)
-
\(f(1)=\dfrac{1+3}{1-1} = \dfrac{4}{0}\text{,}\) which is always undefined.
-
\(\displaystyle f(2)=\dfrac{2+3}{2-1} = \dfrac{5}{1} = 5\)
Notice that in the third question, we discovered that \(f(1)\) is undefined because it results in trying to divide by 0. Remember from Section 8.2 that the domain is all of the possible inputs. Since \(1\) is not a possible input to this function, that means that \(1\) is not in the domain of \(f(x)\text{.}\) However, the numbers we tried that are bigger than 1 and less than 1 were all fine. It was only 1 that caused a problem, because that \(x\)-value made the denominator equal to 0.
Fact 8.4.4. Domain of a Function with Variables in the Denominator.
The domain of a function that has variable in the denominator of a fraction is everything except the \(x\)-values that make the denominator 0.
Example 8.4.5.
Let’s look at the example from the warm-up. Since the only part that can cause problems is the denominator, we can ignore the \(x+3\) in the numerator. We just need to figure out where \(x-1\) is 0, and then our domain will be everything except that number. In other words, we set
\begin{equation*}
x-1 = 0
\end{equation*}
Adding 1 to both sides, we end up with
\begin{equation*}
x = 1
\end{equation*}
Now, remember that we figured out where the denominator is equal to 0, which is where the problem is. However, the domain is everything that isn’t a problem, so our domain will be everything except 1. That means we need to include all the numbers that are bigger than 1 and all the numbers that are less than 1, but just not 1 itself. You might find it helpful to draw a number line. Our final answer in interval notation will be \((-\infty, 1)\cup(1,\infty)\text{.}\)
Checkpoint 8.4.6.
Answer.
\(\left(-\infty,\frac{7}{2}\right)\cup\left(\frac{7}{2},\infty\right)\)
Solution.
Since the only part that can cause problems is the denominator, we can ignore the \(3x+1\) in the numerator. We just need to figure out where \(2x-7\) is 0, and then our domain will be everything except that number. In other words, we set \(2x-7=0\) and solve:
\begin{align*}
2x-7 \amp = 0\\
2x \amp = 7\\
x\amp = \frac{7}{2}
\end{align*}
Now, remember that we figured out where the denominator is equal to 0, which is where the problem is. However, the domain is everything that isn’t a problem, so our domain will be everything except \(\frac{7}{2}\text{.}\) That means we need to include all the numbers that are bigger than \(\frac{7}{2}\) and all the numbers that are less than \(\frac{7}{2}\text{,}\) but just not \(\frac{7}{2}\) itself. You might find it helpful to draw a number line. Our final answer in interval notation will be \((-\infty, \frac{7}{2})\cup(\frac{7}{2},\infty)\text{.}\)
Subsection 8.4.3 Both or Neither
So far, we have learned how to find the domain of a function with a square root of a variable and a function with variables in the denominator. Now, we want to know how to combine them to find the domain of a function that doesn’t have either problem, or a function that has both problems!
Fact 8.4.7. Domain of Square Root in the Denominator.
The domain of a function with a square root of a variable in the denominator of a fraction is where the inside of the square root is strictly greater than 0.The fact above makes sense because it’s a combination of how we dealt with the two problems before. When we just had a square root, we needed the inside to be greater than or equal to 0, because \(\sqrt{0}=0\text{,}\) which isn’t a problem by itself. However, if that square root were in the denominator of a fraction, we would now be trying to divide by 0, which is a problem. That’s why we have to set the inside strictly bigger than 0 in this case.
Example 8.4.8.
Let’s say we want to find the domain of \(f(x)=\dfrac{x+7}{\sqrt{3-x}}\text{.}\) Well, the things that cause a problem here are the square root and the fact that it’s in the denominator. Since the \(x+7\) is not inside the square root and it’s not in the denominator, we can ignore that part. We need to set \(3-x \gt 0\) and solve. There are two ways you could solve it: either by adding \(x\) to both sides, or by subtracting 3 from both sides and then dividing by \(-1\) and flipping the inequality. In either case, we get that our domain is all numbers less than 3. In iterval notation, that means our final answer is \((-\infty,3)\text{.}\)
Checkpoint 8.4.9.
Answer.
\(\left(-\frac{2}{3},\infty\right)\)
Solution.
The things that cause a problem here are the square root and the fact that it’s in the denominator. Since the \(2-x\) is not inside the square root and it’s not in the denominator, we can ignore that part. We need to set \(2+3x \gt 0\) and solve:
\begin{align*}
2+3x \amp\gt 0\\
3x \amp\gt -2\\
x \amp\gt -\frac{2}{3}
\end{align*}
When we turn our answer into interval notation, we get \(\left(-\frac{2}{3},\infty\right)\)
Now that you’ve seen how to handle functions that have both problems, let’s talk about how to handle functions that don’t have either problem.
Fact 8.4.10. Domain without Problems.
The domain of a function that doesn’t have a square root of a variable or a variable in the denominator is everything: \((-\infty, \infty)\text{.}\)Remember: the domain is everything that doesn’t cause a problem. Right now, the only problems we are concerned about are square roots of variables and variables in the denominator of a fraction. If neither of those are there, there is nothing to cause problems, so the domain is just everything!
Example 8.4.11.
Suppose we want to find the domain of \(f(x)=\frac{5}{3}x-\sqrt{7}\text{.}\) Even though we do have a fraction and a square root, they don’t cause problems in this case, because they don’t have any variables. The denominator of the fraction is 3, which is just always 3 and is never 0, so that’s not a problem. Similarly, the inside of our square root is 7, which is always just 7 and is never negative. So, that’s not a problem either. Since this function doesn’t have any problems, the domain is everything: \((-\infty, \infty)\text{.}\)
Checkpoint 8.4.12.
Answer.
\((-\infty, \infty)\)
Solution.
Even though we do have a fraction and a square root, they don’t cause problems in this case, because they don’t have any variables. The denominator of the fraction is 2, which is just always 2 and is never 0, so that’s not a problem. Similarly, the inside of our square root is 8, which is always just 8 and is never negative. So, that’s not a problem either. Since this function doesn’t have any problems, the domain is everything: \((-\infty, \infty)\text{.}\)
Remark 8.4.13.
It is worth noting that you could build more complicated functions that have other problems with the domain. We just aren’t worried about most of them in this class. The only other problem we’re going to deal with is logarithms, but we won’t worry about that until later in the semester.
Subsection 8.4.4
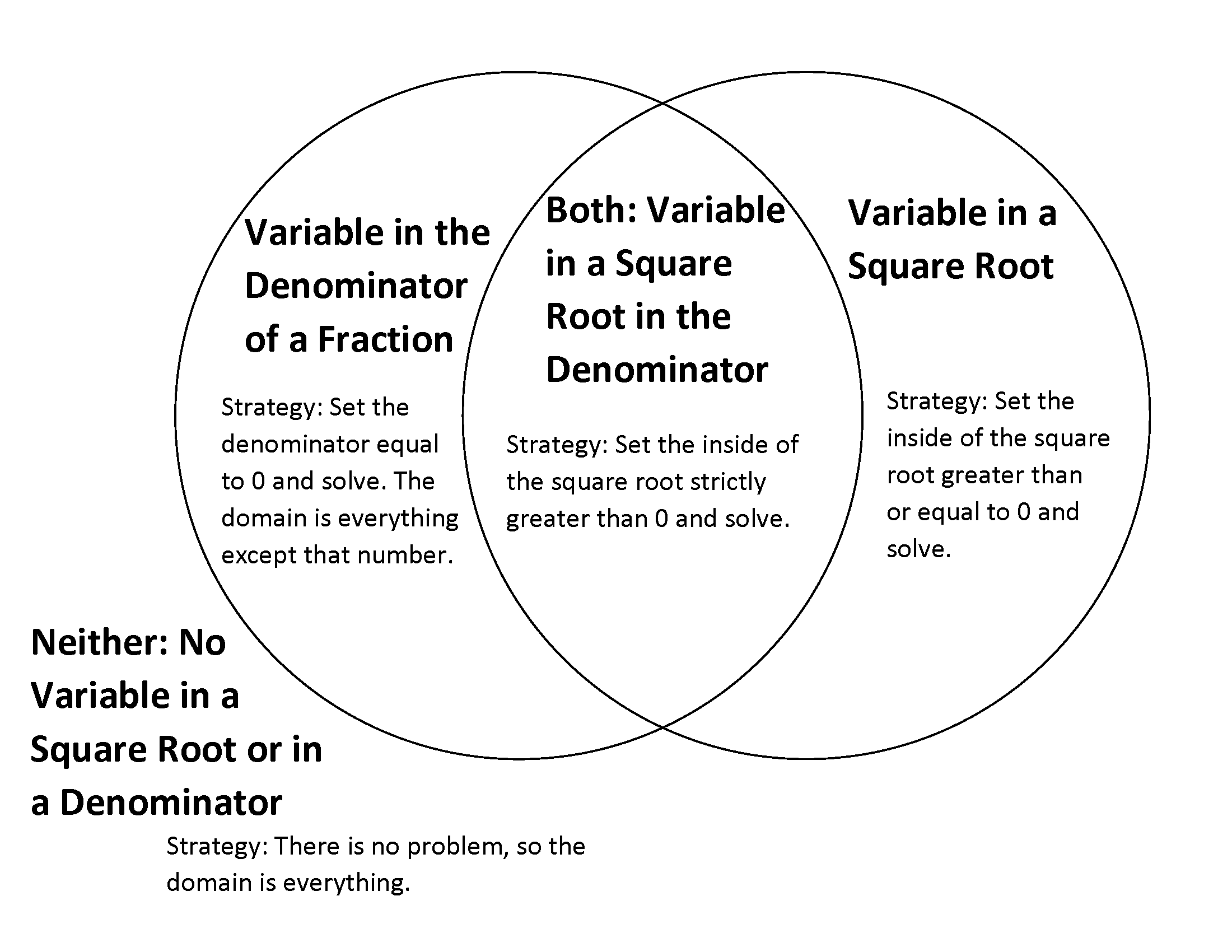
There are four cases we talked about in this section:
-
Square root of a variable: Set the inside of the square root greater than or equal to 0 and solve.
-
Variable in the denominator of a fraction: Set the denominator equal to 0 and solve. The domain is everything except that number.
-
Square root of a variable in the denominator of a fraction: Set the inside of the square root strictly greater than 0 and solve.
-
No square roots of variables or variables in the denominator of a fraction: No problems, so the domain is everything.
You might find it helpful or organize the information here as a Venn diagram, like the one below: