MA 109 Student Guide

Section 3.2 Domain from a Graph

Let's start with a warm-up question. Suppose \(f(x)\) is given in the graph below.

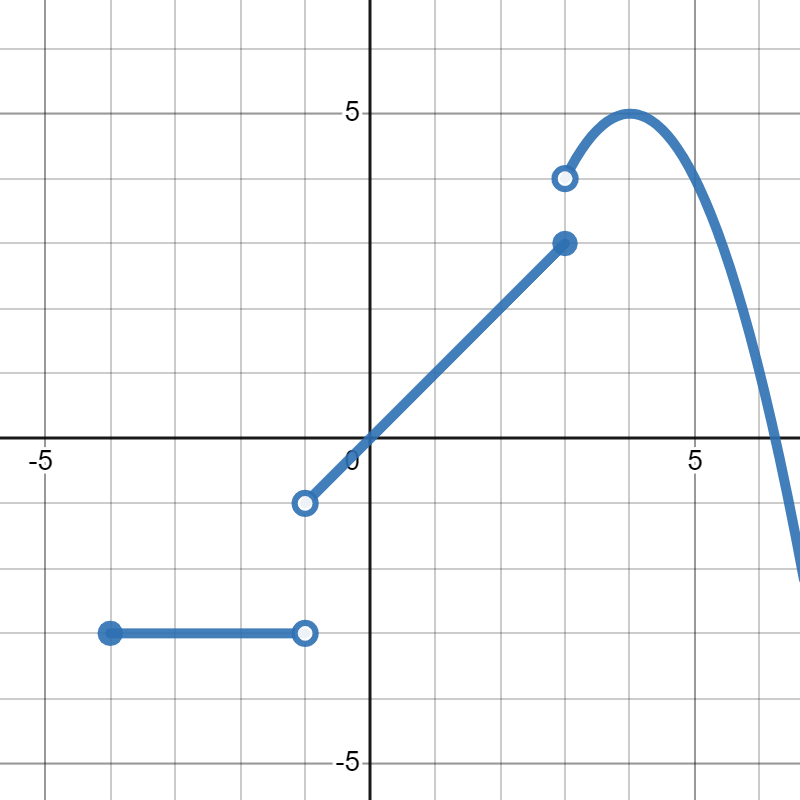
Now, let's say we want to find the following values:

1. \(\displaystyle f(-2)\)

2. \(\displaystyle f(3)\)

3. \(\displaystyle f(-1)\)

For each of these questions, the number given is the input, so it's the \(x\)-value, and we use the graph to find the ouput, or \(y\)-value. For example, to find \(f(-2)\text{,}\) we go to where \(x=-2\) and we see that the corresponding point on the graph is at \((-2,-3)\text{.}\) So, \(f(-2)=-3\text{.}\) We can do the same thing for the second one to see that \(f(3)=3\text{,}\) since we only include the filled-in circles. The point at \((3,4)\) is an open circle, so it's not actually included as part of the graph. When we try to find \(f(-1)\text{,}\) we find just two open circles, so there is no point on the graph at \(x=-1\text{.}\) That means that \(f(-1)\) is undefined.

In the warm-up example above, the first two inputs were included in the graph, but the third input wasn't included. In this section, we want to figure out what are all the possible inputs to a function as a graph.

Remember that when we are looking at a graph of a function, the inputs are the \(x\)-values. So, when we are finding the domain of a graph, we are looking for all of the \(x\)-values that get overed on the graph. There are two metaphors you might find helpful.

• Imagine rain going from the graph to the \(x\)-axis.

• Imagine putting your hands above and below the graph and squishing it onto the \(x\)-axis.

In either case, the endpoints fall to the \(x\)-axis with the same type (open stays open and closed stays closed). Don't forget to write your final answer in interval notation. See the two examples below for an animation of each metaphor and decide which one makes more sense to you.

Checkpoint 3.12.

Find the domain of the function in the graph below: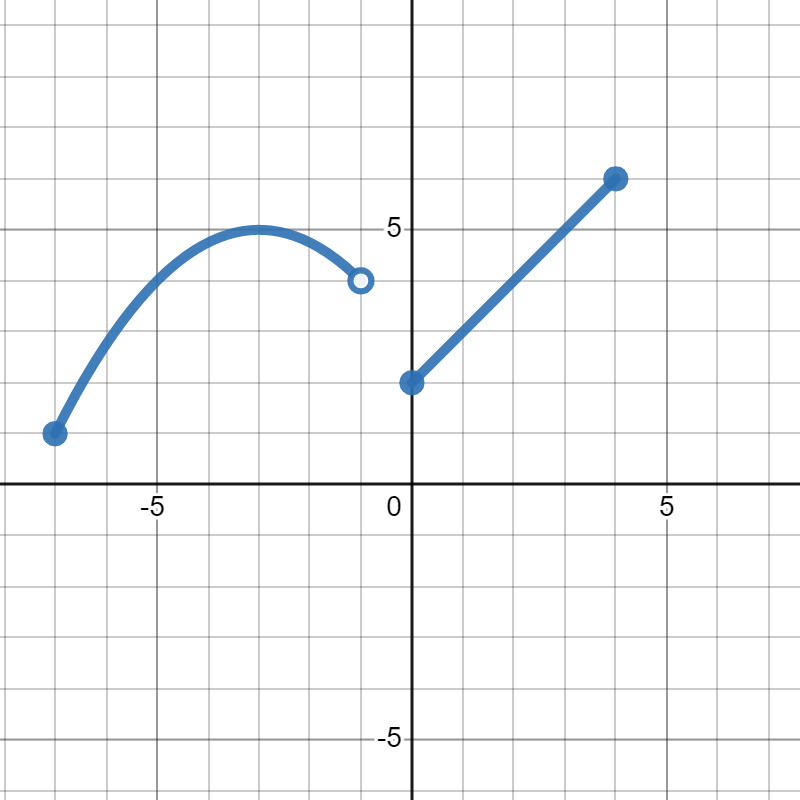

Answer.

\([-7,-1)\cup[0,4]\)

Solution.

First, we look for all of the \(x\)-values that get covered by the graph. We see that the first part starts at \(x=-7\) and ends at \(x=-1\text{,}\) so that will be our first interval. Since the dot at \((-7,1)\) is a closed dot, it is included in the graph, so we need a square bracket \([\) at the \(x=-7\) endpoint of our interval notation. Since the dot at \((-1,4)\) is an open dot, it is not included in the graph, so we need a round parentheses \()\) at the \(x=-1\) end of our interval, giving us \([-7,-1)\) for our first piece.

For the next piece, we see that the graph goes from \(x=0\) to \(x=4\text{.}\) Since both endpoints are closed, they both get square brackets, giving us \([0,4]\) for our other interval.

To put the two intervals together, we use a union. So, our final answer is \([-7,-1)\cup[0,4]\)

Checkpoint 3.14.

Find the domain of the function in the graph below: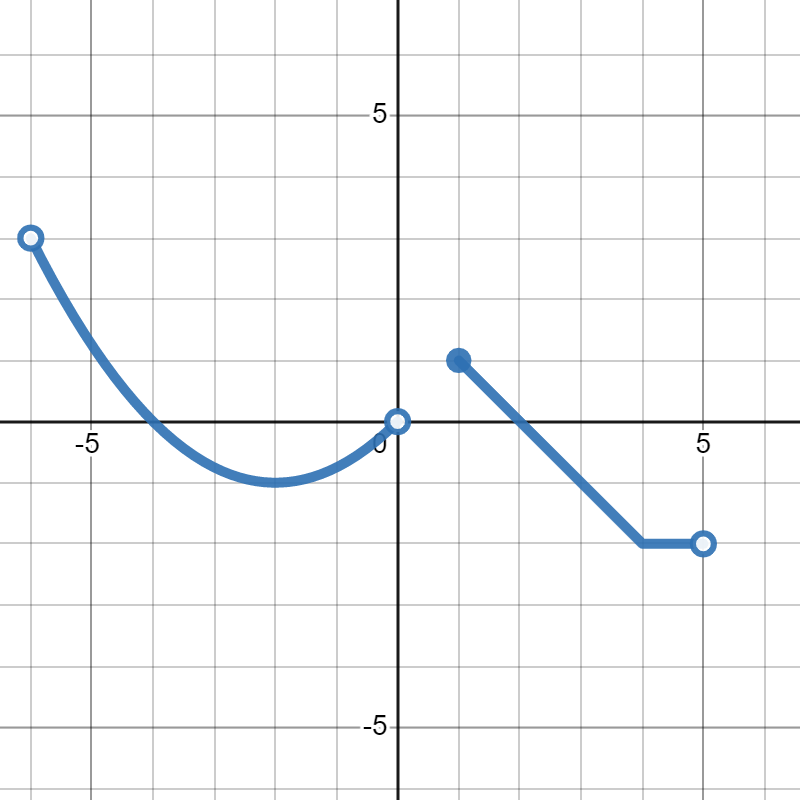

Answer.

\((-6,0)\cup[1,5)\)

Solution.

First, we look for all of the \(x\)-values that get covered by the graph. We see that the first part starts at \(x=-6\) and ends at \(x=0\text{,}\) so that will be our first interval. Since both endpoints of the first part are open, they are not included. So, we need round parentheses for both ends, giving us \((-6,0)\) for our first piece.

For the next piece, we see that the graph goes from \(x=1\) to \(x=5\text{.}\) Since the first endpoint is closed, it is included so it needs a square bracket \([\text{.}\) Since the second endpoint is open, it is not included so it needs a round parentheses \()\text{.}\) This gives us \([1,5)\) for our other interval.

To put the two intervals together, we use a union. So, our final answer is \((-6,0)\cup[1,5)\)

One thing we have to be careful about when there are multiple pieces: if the endpoints overlap, a closed dot can override an open dot, so that \(x\)-value would be included in our domain. This is like how we found \(f(3)\) in the warm-up example at the start of this section. See the example below.

However, if there are two open dots, they don't cancel out. That point just isn't included in our domain. This is like how we found that \(f(-1)\) was undefined in the warm-up example at the start of this section. See the example below.