Section 5.4 Horizontal Scales
Example 5.43. Warm-up.
Suppose \(f(x)\) is given in the table below:
| \(x\) | \(f(x)\) |
| \(-1\) | \(2\) |
| \(0\) | \(3\) |
| \(1.3\) | \(-4\) |
| \(7\) | \(0\) |
| \(14\) | \(1\) |
Now, let's define a new function \(g(x)=f(2x)\text{.}\) We want to construct the table for \(g(x)\text{.}\) Let's follow the same logic we had for the warm-up in section Section 5.3: to fill in the top row, we need to find \(g(-1)\text{.}\) Based on our definition of \(g(x)\text{,}\) we have that \(g(-1)=f(-2(1))=f(-2)\text{.}\) However, at this point we are stuck, because \(x=-2\) is not in our table for \(f(x)\text{.}\) So, we cannot use the same input values for \(g(x)\text{.}\) Instead, we need to reverse engineer what inputs we can use for \(g(x)\) that will match up to the inputs we have for \(f(x)\text{.}\) For example, we know what \(f(-1)\) is, and \(g\left(-\frac{1}{2}\right)=f(2\left(\frac{1}{2}\right))=f(-1)\text{,}\) that means we can use \(-\frac{1}{2}\) as one of our inputs for \(g(x)\) and we have that \(g\left(-\frac{1}{2}\right)=2\text{.}\) We can follow the same logic to get the rest of the table:
| \(x\) | \(g(x)\) |
| \(-\frac{1}{2}\) | \(2\) |
| \(0\) | \(3\) |
| \(0.65\) | \(-4\) |
| \(\frac{7}{2}\) | \(0\) |
| \(7\) | \(1\) |
Let's compare the two functions we looked at in the warm-up example:
| \(x\) | \(f(x)\) |
| \(-1\) | \(2\) |
| \(0\) | \(3\) |
| \(1.3\) | \(-4\) |
| \(7\) | \(0\) |
| \(14\) | \(1\) |
| \(x\) | \(f(2x)\) |
| \(-\frac{1}{2}\) | \(2\) |
| \(0\) | \(3\) |
| \(0.65\) | \(-4\) |
| \(\frac{7}{2}\) | \(0\) |
| \(7\) | \(1\) |
In this case, we were changing the inputs, rather than the outputs. This should make sense because in our formula, the \(2\) is on the inside of the function. The other weird thing you might notice is that although we might expect multiplying by \(2\) to make things bigger, it actually made our \(x\)-values smaller.
In \(f(2x)\text{,}\) all of the inputs are divided by \(2\text{.}\) Remember that on a graph, the inputs are represented by the \(x\)-values, so this would squish all of the \(x\)-values by a factor of \(2\text{.}\) So, the graph of \(f(2x)\) would be the same as the graph of \(f(x)\text{,}\) but squished left/right (towards the \(y\)-axis) by \(2\text{.}\)
Definition 5.48. Horizontal Scales.
The graph of \(f(bx)\) is the same as the graph of \(f(x)\text{,}\) but:
if \(b \gt 1\text{,}\) the graph is squished/compressed towards the \(y\)-axis.
if \(0 \lt b \lt 1\text{,}\) the graph is stretched away from the \(y\)-axis.
We call this a horizontal scale, since "horizontal" means "side-to-side". Notice that the horizontal scales go backwards from what we might expect.
Just as with the vertical scales, we are only looking at positive values of \(b\text{.}\) We'll look at what happens when we multiply by a negative number in Section Section 5.5.
See below for an animation of what this transformation does to a graph. If you want to see the animation in a larger window, click here 12 .
Example 5.49.
Below is the graph of \(h(x)\text{:}\)
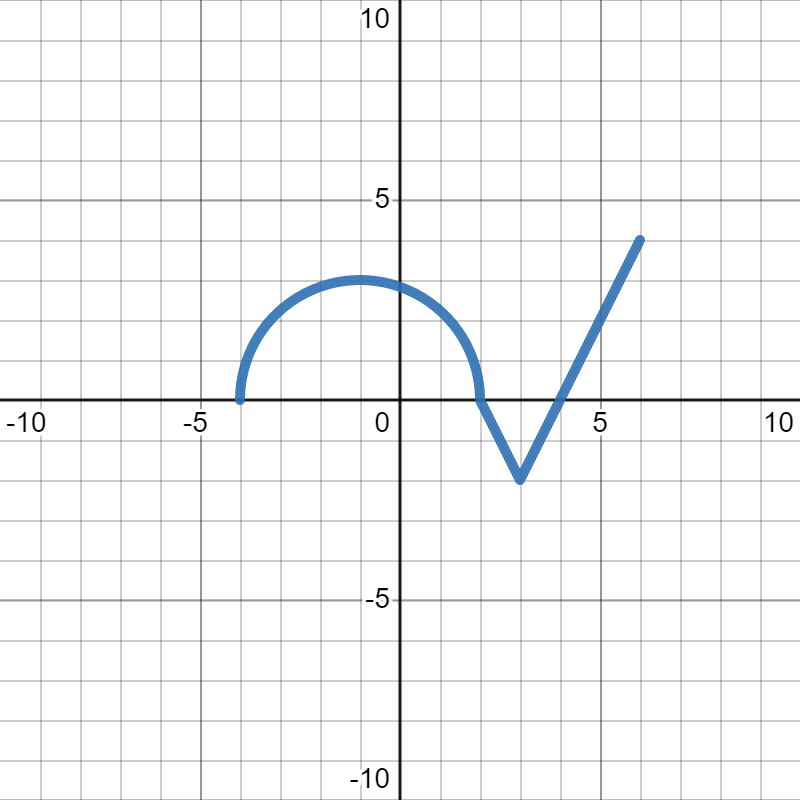
We want to figure out which of the following is the graph of \(h(2x)\text{.}\) In each, the gray dotted graph is the orignal graph of \(h(x)\) so you can more easily see how it changed.
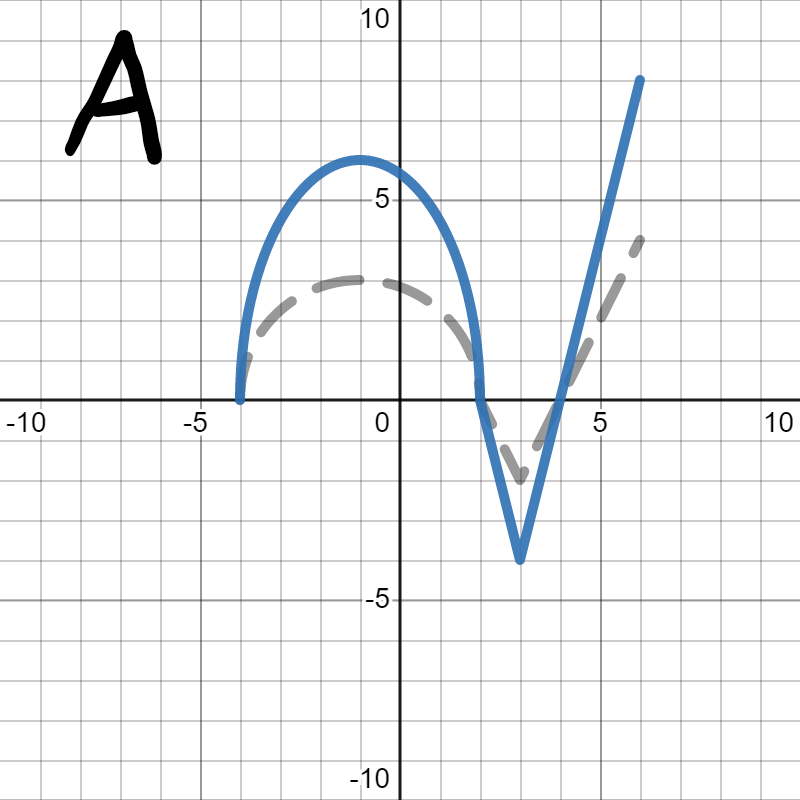
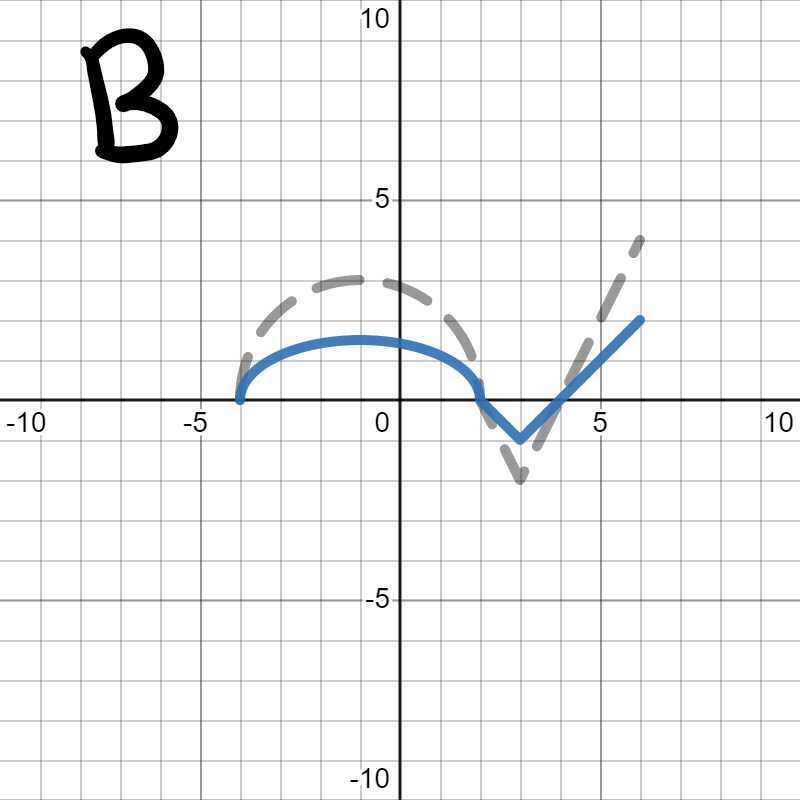
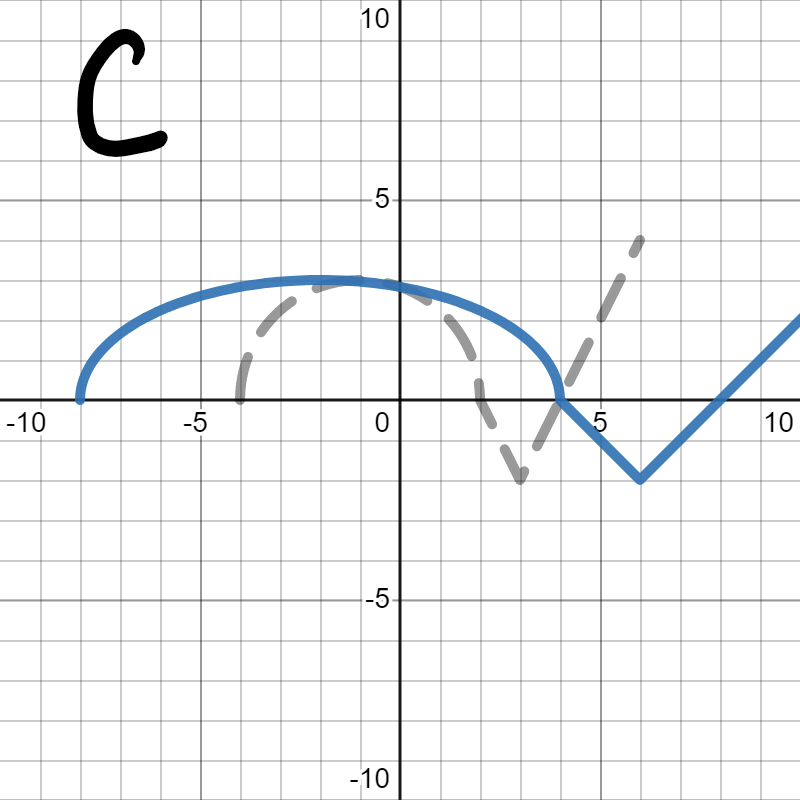
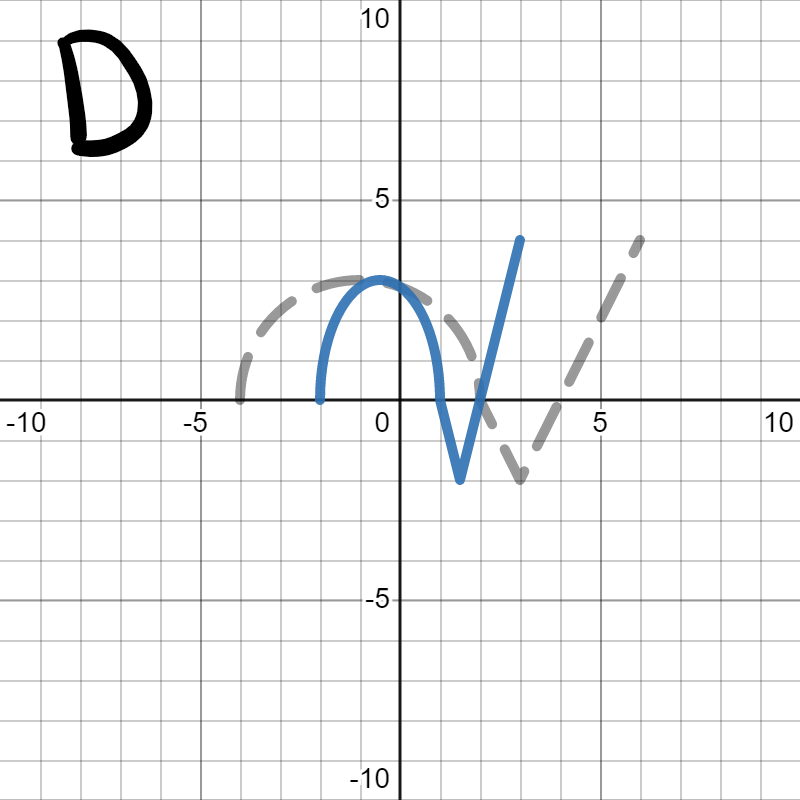
Since we are looking for \(h(2x)\text{,}\) we are looking for the graph to squish horizontally (towards the \(y\)-axis) by 2, which is graph D. Graph A stretched vertically, which we learned in Section 5.3 would be \(2h(x)\text{.}\) Graph B compressed vertically, which we learned in Section 5.3 would be \(\frac{1}{2}h(x)\text{.}\) Graph C stretched horizontally, which would be \(f\left(\frac{x}{2}\right)\text{.}\)
Checkpoint 5.50.
The graph of \(p(x)\) is below:
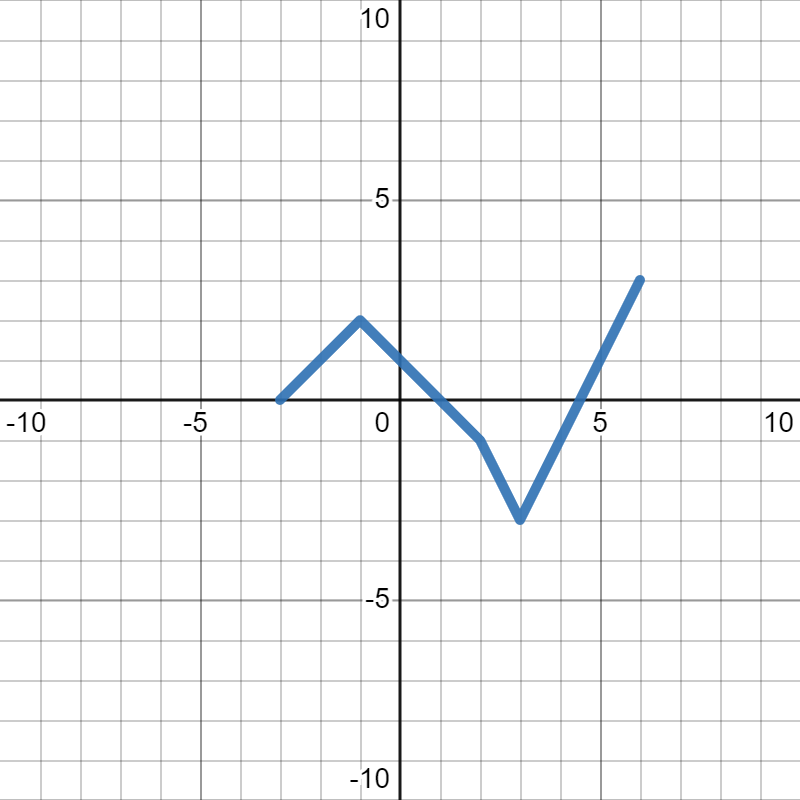
Sketch the graph of each of the following:
\(\displaystyle p(3x)\)
\(\displaystyle p\left(\frac{1}{2}x\right)\)
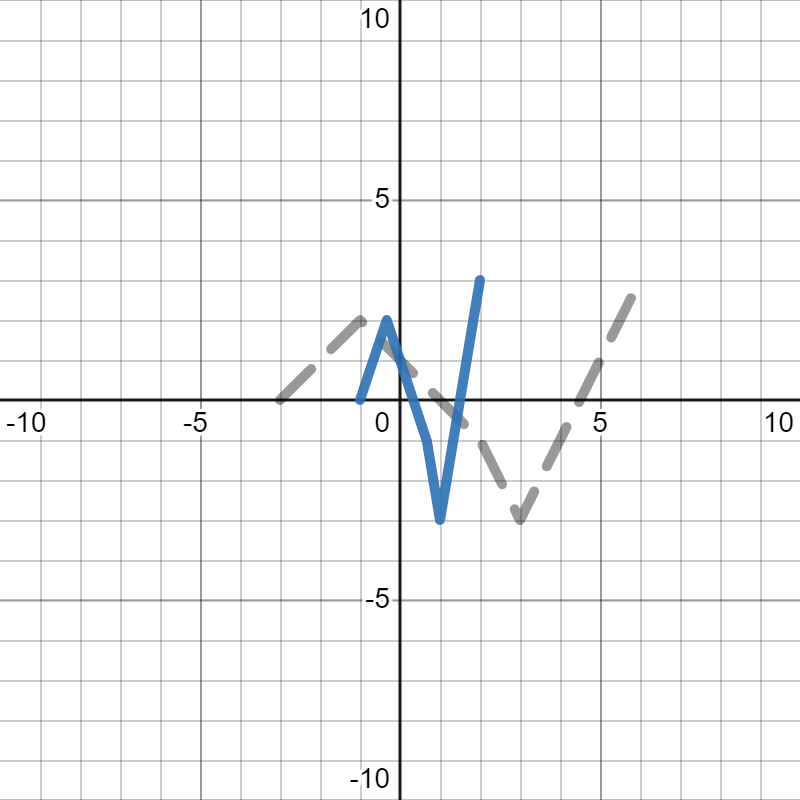
- To draw \(p(3x)\text{,}\) we see that we are squishing the whole graph horizontally by 3 (towards the \(y\)-axis). Since we are dividing all the \(x\)-values by 3, and \(0\) times anything is still \(0\text{,}\) the point on the \(y\)-axis (where \(x=0\)) stays where it is at. Next, we will move the corner points, then connect them together to get the whole graph. So, you would move the point \((-3,0)\) on the original graph over to \((-1,0)\text{.}\) Similarly, you would move the point \((-1,2)\) on the original graph over to \((-\frac{1}{3},2)\text{,}\) move the point \((2,-1)\) on the original graph over to \((\frac{2}{3},-1)\text{,}\) move the point \((3,-3)\) on the original graph over to \((1,-3)\text{,}\) and move the point \((6,3)\) on the original graph over to \((2,3)\text{.}\) From there, you can connect the lines to get the final graph, shown in blue below, where the gray dotted line is the orignal graph of \(p(x)\text{.}\)
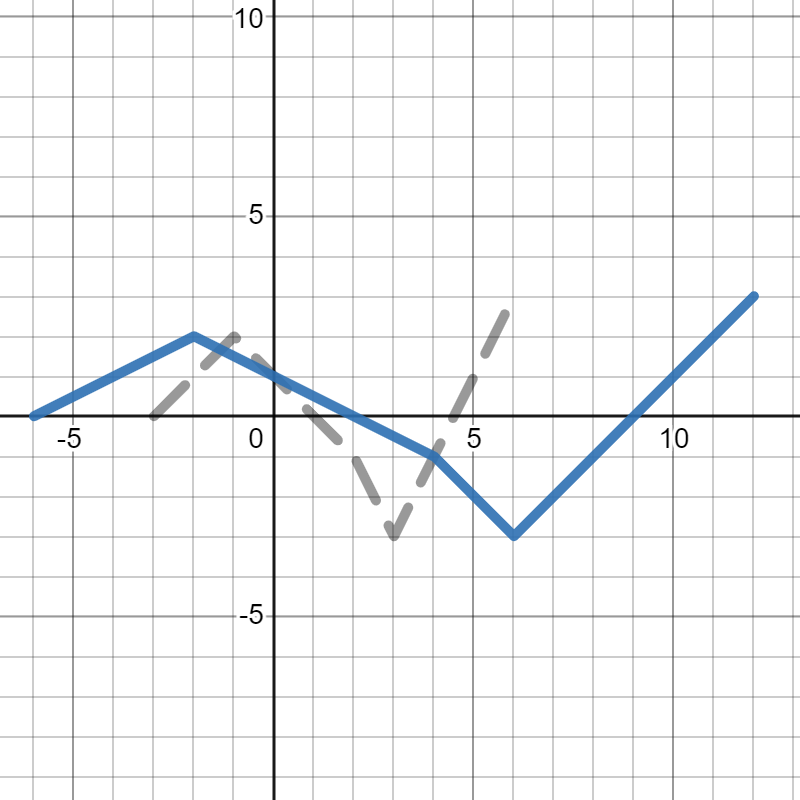
- To draw \(p\left(\frac{1}{2}x\right)\text{,}\) we see that we are stretching the whole graph horizontally by 2 (away from the \(y\)-axis). Since we are multiplying all the \(x\)-values by 3, and \(0\) times anything is still \(0\text{,}\) the point on the \(y\)-axis (where \(x=0\)) stays where it is at. Next, we will move the corner points, then connect them together to get the whole graph. So, you would move the point \((-3,0)\) on the original graph over to \((-6,0)\text{.}\) Similarly, you would move the point \((-1,2)\) on the original graph over to \((-2,2)\text{,}\) move the point \((2,-1)\) on the original graph over to \((4,-1)\text{,}\) move the point \((3,-3)\) on the original graph over to \((6,-3)\text{,}\) and move the point \((6,3)\) on the original graph over to \((12,3)\text{.}\) From there, you can connect the lines to get the final graph, shown in blue below, where the gray dotted line is the orignal graph of \(p(x)\text{.}\)
Example 5.51.
Suppose the solid blue graph below is the graph of \(f(x)\) and the dotted red graph is the graph of \(g(x)\text{:}\)
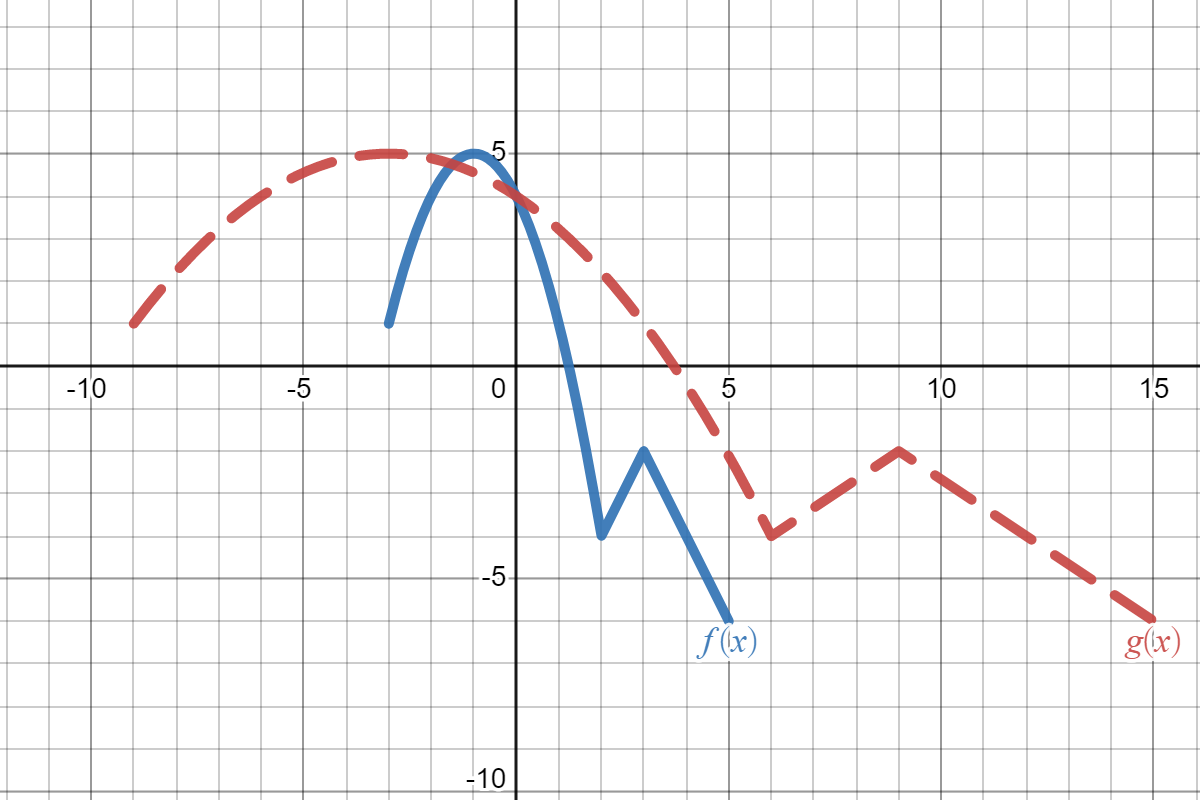
We want to write a formula for \(g(x)\) in terms of \(f(x)\text{.}\) In other words, we start with \(f(x)\) and figure out how the graph changed to get to \(g(x)\text{,}\) then write how that changes the formula. Since the question asks for the formula "in terms of \(f(x)\)", that means we will write \(f(x)\) somewhere in our answer. Looking at the graph, we see that \(g(x)\) is the graph of \(f(x)\) stretched horizontally (away from the \(y\)-axis) by \(3\text{.}\) Therefore, that means we are dividing by \(3\) inside of the function \(f(x)\text{.}\) So, our final answer is \(g(x)=f\left(\frac{x}{3}\right)\text{.}\)
Checkpoint 5.52.
Suppose the solid blue graph below is the graph of \(f(x)\) and the dotted red graph is the graph of \(g(x)\text{:}\)
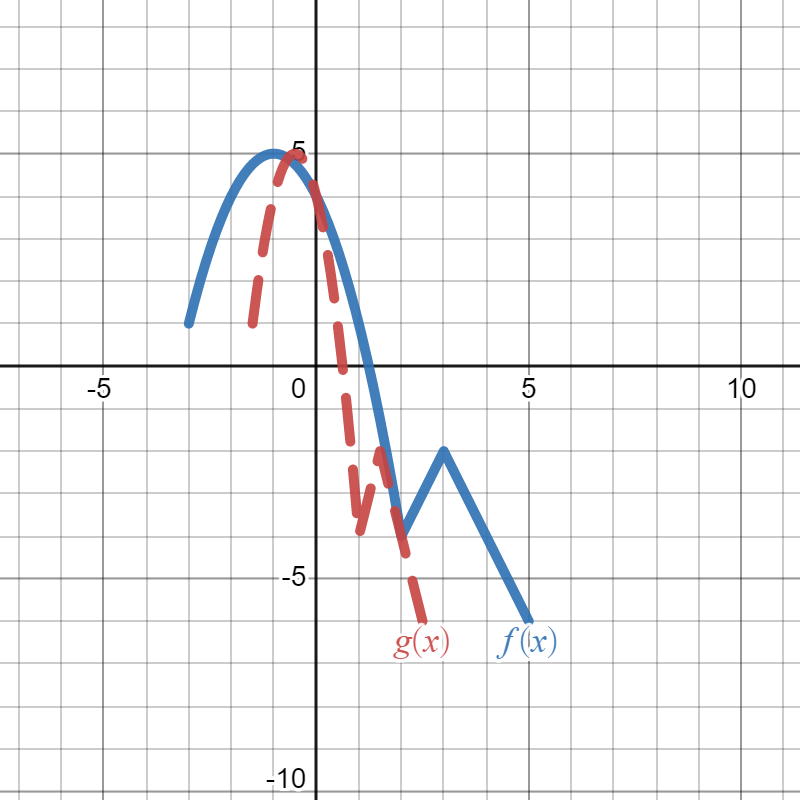
Write a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
\(g(x)=f(2x)\)
We want to write a formula for \(g(x)\) in terms of \(f(x)\text{.}\) In other words, we start with \(f(x)\) and figure out how the graph changed to get to \(g(x)\text{,}\) then write how that changes the formula. Since the question asks for the formula "in terms of \(f(x)\)", that means we will write \(f(x)\) somewhere in our answer. Looking at the graph, we see that \(g(x)\) is the graph of \(f(x)\) squished horizontally (towards the \(y\)-axis) by \(2\text{.}\) Therefore, that means we are multiplying by \(2\) inside of the function \(f(x)\text{.}\) So, our final answer is \(g(x)=f(2x)\text{.}\)
Example 5.53.
Suppose \(f(x)=x^2+3x-4\) and \(g(x)\) is the same as \(f(x)\) but stretched horizontally by \(7\text{.}\) Let's write a formula for \(g(x)\text{.}\) Since we have an explicit formula for \(f(x)\) in this case, we can write an explicit formula for \(g(x)\text{,}\) too. Since we are stretching horizontally by \(7\text{,}\) that means we are dividing by \(7\) to the inside of the function. So,
So our final answer is \(g(x)=\left(\frac{x}{7}\right)^2+3\left(\frac{x}{7}\right)-4\text{.}\)
Checkpoint 5.54.
Suppose \(f(x)=3x^3-2x+1\) and \(g(x)\) is the same as \(f(x)\) but squished horizontally by \(4\text{.}\) Write a formula for \(g(x)\text{.}\)
\(g(x)=3(4x)^3-2(4x)+1\)
Since we have an explicit formula for \(f(x)\) in this case, we can write an explicit formula for \(g(x)\text{,}\) too. Since we are squishing horizontally by \(4\text{,}\) that means we are multiplying by \(4\) on the inside of the function. So,
So our final answer is \(g(x)=3(4x)^3-2(4x)+1\text{.}\)
Example 5.55.
Suppose \(f(x)=x^2-x+5\) and \(g(x)=(3x)^2-(3x)+55\text{.}\) Let's figure out what transformations took \(f(x)\) to \(g(x)\text{.}\) Comparing the two formulas, we see that in the formula for \(g(x)\text{,}\) all of the \(x\)'s turned into \((3x)\text{.}\) That means that to get from \(f(x)\) to \(g(x)\text{,}\) we must have multiplied by \(3\) on the inside so that \(g(x)=f\left(3x\right)\text{.}\) That means there was a horizontal squish by \(3\text{.}\)
Checkpoint 5.56.
Suppose \(f(x)=3x+2\) and \(g(x)=3\left(\frac{x}{5}\right)+2\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
Horizontal stretch by \(5\text{.}\)
Comparing the two formulas, we see that in the formula for \(g(x)\text{,}\) all of the \(x\)'s were replaced with \(\left(\frac{x}{5}\right)\text{.}\) That means that to get from \(f(x)\) to \(g(x)\text{,}\) we must have divided by \(5\) on the inside so that \(g(x)=f\left(\frac{x}{5}\right)\text{.}\) That means there was a horizontal stretch by \(5\text{.}\)
https://www.desmos.com/calculator/1yxhjje7no