Skip to main content

Section 6.3 Domain and Range of an Inverse

Remember that the domain of a function is all of the possible inputs and the range of a function is all of the possible outputs. Since the inverse swaps inputs and outputs, the inverse will also swap the domain and range.

Example 6.12.

Suppose we have a function \(g(x)\text{,}\) and we know that its domain is \([-4,7)\) and its range is \([0,\infty)\text{.}\) Then:

  • The domain of \(g^{-1}(x)\) is \([0,\infty)\) (since that is the range of \(g(x)\)).

  • The range of \(g^{-1}(x)\) is \([-4,7)\) (since that is the domain of \(g(x)\)).

Checkpoint 6.13.

Suppose the function \(G(x)\) is graphed below:

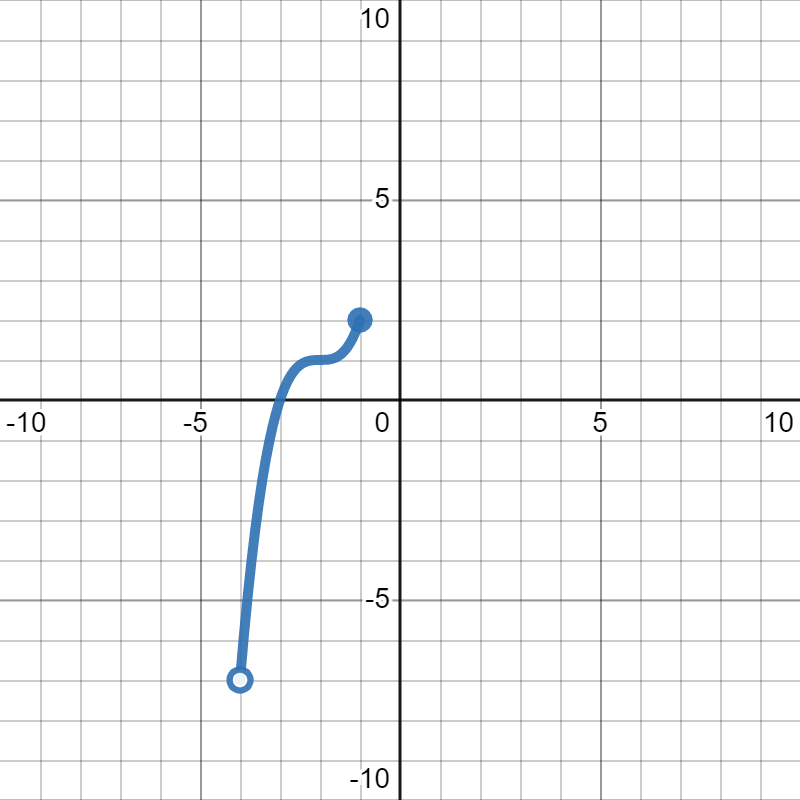
Find each of the following:

  1. The domain of \(G(x)\text{.}\)

  2. The range of \(G(x)\text{.}\)

  3. The domain of \(G^{-1}(x)\text{.}\)

  4. The range of \(G^{-1}(x)\text{.}\)

Solution.

  1. The domain of this graph is \((-4,-1]\text{.}\) For a review of how to find the domain of a grpah, see Section Section 3.2.

  2. The range of this graph is \((-7,2]\text{.}\) For a review of how to find the range of a grpah, see Section Section 3.3.

  3. To find the domain of \(G^{-1}(x)\text{,}\) we have to remember that it's the same as the range of \(G(x)\text{.}\) We already found the range of the original function, so we have our answer: the domain of \(G^{-1}(x)\) is \((-7,2]\text{.}\)

  4. To find the range of \(G^{-1}(x)\text{,}\) we have to remember that it's the same as the domain of \(G(x)\text{.}\) We already found the domain of the original function, so we have our answer: the range of \(G^{-1}(x)\) is \((-4,-1]\text{.}\)

A natural question you might be asking yourself is: when would this be useful? We are going to discuss one example. Look back at Chapter Chapter 3. The chapter was about domain and range. We began by looking at graphs, first finding the domain of a graph and then finding the range of a graph. After that, we moved on to functions as formulas, but we only looked at finding the domain of a function. We never talked about how to find the range of a function. The reason is that it is much more complicated, and there is a lot more variation between functions. Unlike with domain, there aren't a few nice categories you can fit functions into when finding their range. You basically have to look at each function separately, and some are very hard to figure out without just graphing it. However, we just learned that the range of a function is the same as the domain of its inverse. So, if we can find the inverse and find its domain, that's a nice trick for finding the range.

Example 6.14. Using Inverses to Find Range.

Suppose we have the function \(f(x)=\dfrac{x-1}{3x+2}\) and we want to find its range. We don't have a nice way to find range from a formula, but we do know that the range will be the same as the domain of the inverse. So, our strategy will be to find a formula for \(f^{-1}(x)\) and then find its domain.

Remember from Section Section 6.2 that to find the formula for the inverse, we write \(y=\dfrac{x-1}{3x+2}\text{,}\) swap \(x\) and \(y\text{:}\) \(x= \dfrac{y-1}{3y+2}\text{,}\) and then solve for \(y\text{:}\)

\begin{align*} x \amp= \dfrac{y-1}{3y+2}\\ x(3y+2)\amp= y-2\\ 3xy+2x \amp = y-2\\ 3xy-y+2x \amp = -2\\ 3xy-y \amp= -2x-2\\ y(3x-1) \amp = -2x-2\\ y \amp= \dfrac{-2x-2}{3x-1} \end{align*}

For a detailed description of the algebra above, see exercise Checkpoint 6.10.

Now that we have our inverse function \(f^{-1}(x)=\dfrac{-2x-2}{3x-1}\text{,}\) we need to find its domain. Remember from Section Section 3.4 that to find the domain, we look for the problems. In this case, the problem is that we have a variable in the denominator. Since we can never divide by \(0\text{,}\) we need to figure out where the denominator is \(0\text{,}\) and then our domain will be everything except that.

\begin{align*} 3x-1 \amp = 0\\ 3x \amp = 1\\ x \amp = \frac{1}{3} \end{align*}

So, our domain is everything except \(\frac{1}{3}\text{.}\) That means we want everything less than \(\frac{1}{3}\) and everything greater than \(\frac{1}{3}\text{,}\) which is \((-\infty, \frac{1}{3})\cup(\frac{1}{3},\infty)\text{.}\)

We are now ready to write our final answer. We figured out that \(f^{-1}(x)=\dfrac{-2x-2}{3x-1}\) and that the domain of the inverse is \((-\infty, \frac{1}{3})\cup(\frac{1}{3},\infty)\text{.}\) Since the range of \(f(x)\) is the same as the domain of the inverse, that means the range of \(f(x)\) is \((-\infty, \frac{1}{3})\cup(\frac{1}{3},\infty)\text{.}\)