Skip to main content

Section 11.1 Roots of Quadratic Functions

Definition 11.1.

The roots of a quadratic function are the \(x\)-values of the \(x\)-intercepts. We also sometimes call these the zeros of the function.

Example 11.2.

Suppose \(f(x)\) is the quadratic function graphed below. We want to find the roots of that function.

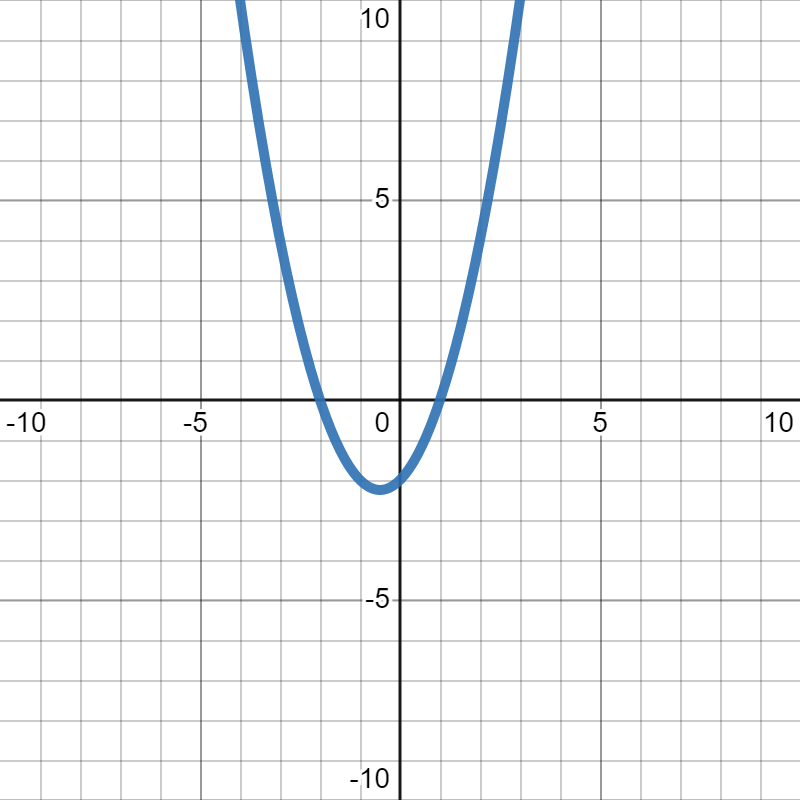
We look at the \(x\)-axis, which crosses the graph at \(x=-2\) and \(x=1\text{,}\) so those are our roots. The answer to this question is \(x=-2,1\text{.}\)

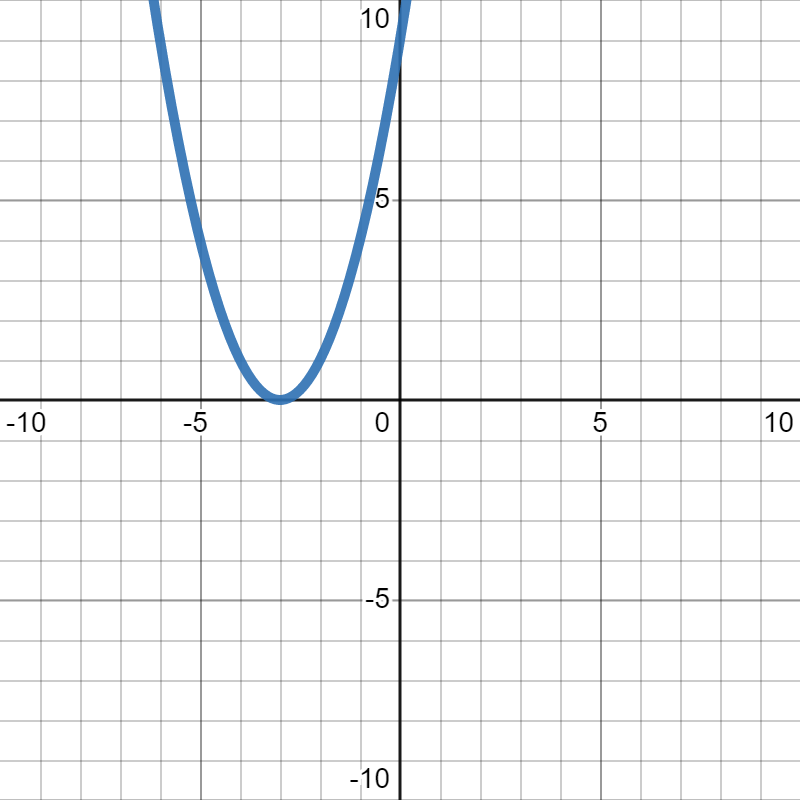
Checkpoint 11.3.

Suppose \(f(x)\) is the quadratic function graphed below. What are the roots of that function?

Answer.
\(x=-3\)
Solution.

To find the roots, we need to look at the \(x\)-axis. We see that it crosses the graph at \(x=-3\text{,}\) and that's it. Therefore, this one only has one root: \(x=-3\text{.}\)

Most of the time, we will be given an equation for the function, and we will need to do algebra to figure out what the roots are, rather than looking at a graph. Since we are just looking for the \(x\)-intercepts, we know from Section 1.2 just need to set \(y=0\) and solve for \(x\text{.}\) The actual solving part, however, requires some new strategies we have not yet discussed. There are three main strategies you need to be aware of, depending on how the function is given. The three examples below each discuss one of those strategies.

Example 11.4. Zero Product Property.

Suppose \(f(x)=3(x+5)(x-2)\text{,}\) and we want to find its roots. As we always do with roots and \(x\)-intercept, we begin by setting \(y=0\text{,}\) so we need to solve the following equation:

\begin{equation*} 0=3(x+5)(x-2) \end{equation*}

Take a close look at the equation: we have a bunch of things multiplied together and it all equals 0. The fact that it equals 0 is special. There is no way to mulitply things together to get 0, unless one of the numbers you multiplied was already 0. This doesn't work for other numbers. For example, 12 can be written as 1 times 12, but it is also 3 times 4 or 2 times 6. But 0 has to have a zero to begin with.

Why does that matter? Because we know one of the things we multiplied had to be 0 to begin with, this lets us separate our first equation into three separate equations:

\begin{align*} 0\amp=3\\ 0\amp=x+5\\ 0\amp=x-2 \end{align*}

The first equation doesn't have any \(x\) in it, and is nonsense since 3 does not equal 0. So that one doesn't help us, we'll ignore it. The second one we can subtract 5 from both sides to get \(x=-5\text{.}\) The third one we can add 2 to both sides to get \(x=2\text{.}\) Therefore, our answer is that this function has two roots: \(x=-5,2\text{.}\)

Checkpoint 11.5.

Suppose \(f(x)=-\frac{1}{2}(x+7)(x-2)\text{.}\) What are the roots of \(f(x)\text{?}\)
Answer.
\(x=-7,2\)
Solution.

As we always do with roots and \(x\)-intercept, we begin by setting \(y=0\text{,}\) so we need to solve the following equation:

\begin{equation*} 0=-\frac{1}{2}(x+7)(x-2) \end{equation*}

Just as we had with the example, we have a bunch of things multiplied together to be 0. That means one of them had to be zero to begin with. Because we know one of the things we multiplied had to be 0 to begin with, this lets us separate our first equation into three separate equations:

\begin{align*} 0\amp=-\frac{1}{2}\\ 0\amp=x+7\\ 0\amp=x-2 \end{align*}

The first equation doesn't have any \(x\) in it, and is nonsense since \(-\frac{1}{2}\) does not equal 0. So that one doesn't help us, we'll ignore it. The second one we can subtract 7 from both sides to get \(x=-7\text{.}\) The third one we can add 2 to both sides to get \(x=2\text{.}\) Therefore, our answer is that this function has two roots: \(x=-7,2\text{.}\)

Example 11.6. Square Root.

Suppose \(f(x)=2(x+4)^2-6\text{,}\) and we want to find the roots of \(f(x)\text{.}\) As we always do with roots and \(x\)-intercept, we begin by setting \(y=0\text{,}\) so we need to solve the following equation:

\begin{equation*} 0=2(x+4)^2-6 \end{equation*}

In this case, there is only one \(x\) floating around in our equation, so we just need to work on getting it by itself. Remember that to solve an equation, we use order of operations, but backwards. So, the \(+4\) is inside parentheses, so that will go last. We deal with everything outside the parentheses first, going from addition/subtraction, then multiplication/division, then the exponent. Don't forget: when we take the square root to get rid of the square, we need the positive and negative!

\begin{align*} 0\amp=2(x+4)^2-6\\ 0{\color{red}{+6}}\amp=2(x+4)^2-6{\color{red}{+6}}\\ 6 \amp= 2(x+4)^2\\ \dfrac{6}{\color{red}{2}}\amp=\dfrac{2(x+4)^2}{\color{red}{2}}\\ 3 \amp=(x+4)^2\\ \pm\sqrt{3}\amp= \sqrt{(x+4)^2}\\ \pm\sqrt{3}\amp=x+4\\ \pm\sqrt{3}{\color{red}{-4}}\amp=x+4{\color{red}{-4}}\\ -4\pm\sqrt{3}\amp=x \end{align*}

Therefore, we have our answer: this function has two roots at \(x=-4+\sqrt{3}, -4-\sqrt{3}\text{.}\)

Checkpoint 11.7.

Suppose \(f(x)=4(x-7)^2-9\text{.}\) What are the roots of \(f(x)\text{?}\)
Answer.

This function has two roots at \(x=\frac{23}{2},\frac{5}{2}\text{.}\) If you prefer decimals, the roots of this function are \(x=11.5, 2.5\text{.}\)

Solution.

As we always do with roots and \(x\)-intercept, we begin by setting \(y=0\text{,}\) so we need to solve the following equation:

\begin{equation*} 0=4(x-7)^2-9 \end{equation*}

In this case, there is only one \(x\) floating around in our equation, so we just need to work on getting it by itself. Remember that to solve an equation, we use order of operations, but backwards. So, the \(-7\) is inside parentheses, so that will go last. We deal with everything outside the parentheses first, going from addition/subtraction, then multiplication/division, then the exponent. Don't forget: when we take the square root to get rid of the square, we need the positive and negative!

\begin{align*} 0\amp=4(x-7)^2-9\\ 0{\color{red}{+9}}\amp=4(x-7)^2-9{\color{red}{+9}}\\ 9 \amp= 4(x-7)^2\\ \dfrac{9}{\color{red}{4}}\amp=\dfrac{4(x-7)^2}{\color{red}{4}}\\ \frac{9}{4} \amp=(x-7)^2\\ \pm\sqrt{\frac{9}{4}}\amp= \sqrt{(x-7)^2}\\ \pm\frac{9}{2}\amp=x-7\\ \pm\frac{9}{2}{\color{red}{+7}}\amp=x-7{\color{red}{+7}}\\ 7\pm\frac{9}{2}\amp=x \end{align*}

We can comine our fractions by getting a common denominator, since \(7=\frac{14}{2}\text{:}\)

\begin{gather*} 7+\frac{9}{2} = \frac{14}{2}+\frac{9}{2}=\frac{23}{2}\\ 7-\frac{9}{2} = \frac{14}{2}-\frac{9}{2}=\frac{5}{2} \end{gather*}

Therefore, we have our answer: this function has two roots at \(x=\frac{23}{2},\frac{5}{2}\text{.}\) If you prefer decimals, the roots of this function are \(x=11.5, 2.5\text{.}\)

The last strategy we will go over involves a formula you may have seen in high school.

Example 11.9.

Suppose \(f(x)=2x^2-3x+1\text{.}\) We want to find the roots of \(f(x)\text{.}\) As we always do with roots and \(x\)-intercept, we begin by setting \(y=0\text{,}\) so we need to solve the following equation:

\begin{equation*} 0=2x^2-3x+1 \end{equation*}

This function is set up with exactly the format we need for the quadratic formula, so that's what we'll use. We look at the equation to see that \(a=2\text{,}\) \(b=-3\text{,}\) and \(c=1\text{.}\) Plugging that in, we get

\begin{align*} x \amp= \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\ x \amp= \dfrac{-(-3)\pm\sqrt{(-3)^2-4(2)(1)}}{2(2)}\\ x\amp = \dfrac{3\pm\sqrt{9-8}}{4}\\ x\amp=\dfrac{3\pm 1}{4} \end{align*}

So, we have two roots:

\begin{gather*} x=\dfrac{3+1}{4} = \dfrac{4}{4} =1\\ x=\dfrac{3-1}{4} = \dfrac{2}{4} =\dfrac{1}{2} \end{gather*}

So, our answer is \(x=1, \frac{1}{2}\text{.}\)

Checkpoint 11.10.

Suppose \(f(x)=x^2+7x+10\text{.}\) What are the roots of \(f(x)\text{?}\)
Answer.
\(x=-2,5\)
Solution.

As we always do with roots and \(x\)-intercept, we begin by setting \(y=0\text{,}\) so we need to solve the following equation:

\begin{equation*} 0=x^2+7x-10 \end{equation*}

This function is set up with exactly the format we need for the quadratic formula, so that's what we'll use. We look at the equation to see that \(a=1\text{,}\) \(b=7\text{,}\) and \(c=10\text{.}\) Plugging that in, we get

\begin{align*} x \amp= \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\ x \amp= \dfrac{-(7)\pm\sqrt{(7)^2-4(1)(10)}}{2(1)}\\ x\amp = \dfrac{-7\pm\sqrt{49-40}}{2}\\ x\amp = \dfrac{-7\pm\sqrt{9}}{2}\\ x\amp=\dfrac{-7\pm 3}{2} \end{align*}

So, we have two roots:

\begin{gather*} x=\dfrac{-7+3}{2} = \dfrac{-4}{2} =-2\\ x=\dfrac{-7-3}{2} = \dfrac{-10}{2} =-5 \end{gather*}

So, our answer is \(x=-2,-5\text{.}\)