Section 2.5 Solving with Functions
The output to a function is what it is equal to. So, when we are given the function as a formula, our strategy will be to set the formula equal to the output and solve for \(x\text{.}\)
Example 2.27.
Suppose \(f(x)=3x-7\) and we want to solve \(f(x)=5\text{.}\) If we had been asked to find \(f(5)\text{,}\) then \(5\) would be our input and we would plug it in for \(x\text{,}\) but instead, the question set \(f(x)\) equal to \(5\text{,}\) which makes \(5\) our output. So, we are going to set our formula equal to the output and solve:
Checkpoint 2.28.
Suppose \(f(x)=\dfrac{x+3}{x-7}\text{.}\)
Solve \(f(x)=2\text{.}\)
Evaluate \(f(2)\text{.}\)
\(\displaystyle x=17\)
\(f(2)=-1\text{.}\)
Suppose \(f(x)=\dfrac{x+3}{x-7}\text{.}\)
To solve \(f(x)=2\text{,}\) we see that \(2\) is our output. So, we set the formula equal to the output and solve for \(x\text{:}\)
\begin{align*} \dfrac{x+3}{x-7} \amp =2\\ x+3 \amp =2(x-7)\\ x+3 \amp =2x-14\\ -x+3 \amp =-14\\ -x \amp = -17\\ x \amp = 17 \end{align*}To evaluate \(f(2)\text{,}\) we see that \(2\) is our input, since it is inside the parentheses. So, we replace \(x\) in the formula with \(2\text{:}\)
\begin{equation*} f(2) = \dfrac{(2)+3}{(2)-7} = \dfrac{5}{-5} = -1 \end{equation*}
When we are given the function as a graph, we remember that the inputs are represented by the \(x\)-values, and the outputs are represented by the \(y\)-values. So, when we are given the output, that means we are given the \(y\)-value, and we need to find the \(x\)-value(s) that correspond to it. Note that there could be more than one!
Example 2.29.
Let \(g(x)\) be given in the graph below:
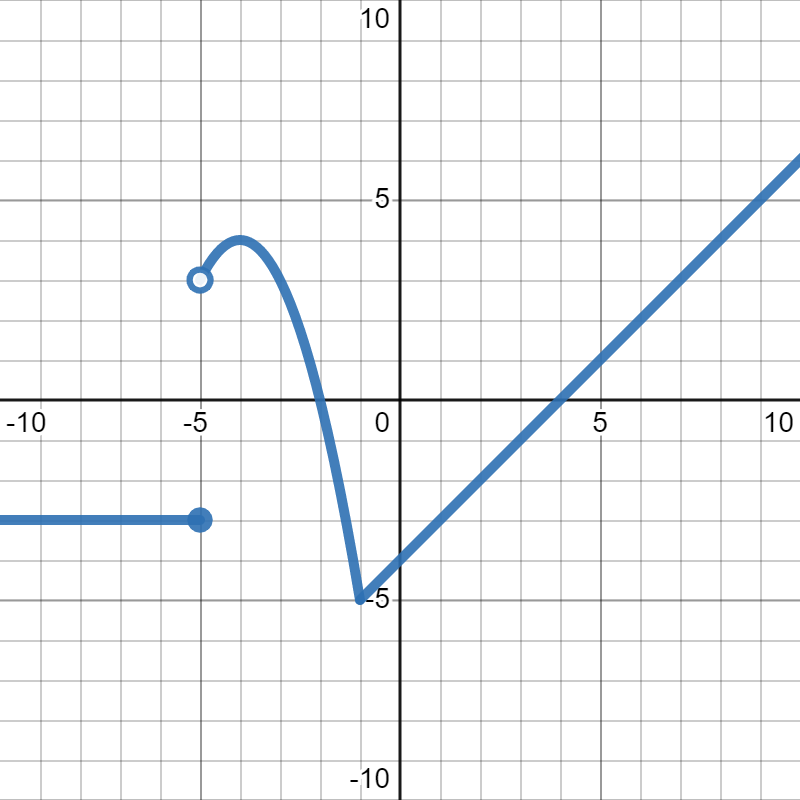
Suppose we want to solve \(g(x)=3\text{.}\) Since \(3\) is our output, that means it's our \(y\)-value. So, we move up the \(y\)-axis to where \(y=3\) and look left and right to see where it crosses the graph. We find three points that have \(y=3\text{:}\) \((-5,3)\text{,}\) \((-3,3)\text{,}\) and \((7,3)\text{.}\) However, because \((-5,3)\) is an open circle, it is not included in the graph, so we can ignore it. In this case, we are looking for the inputs, which are the \(x\)-values, so we have two answers: \(x=-3,7\text{.}\)
Checkpoint 2.30.
Let \(g(x)\) be given in the graph below:

Solve each of the following:
\(\displaystyle g(x)=0\)
\(\displaystyle g(x)=5\)
\(\displaystyle g(x)=-7\)
\(\displaystyle x=-2,4\)
\(\displaystyle x=\)
none
Solve each of the following:
To solve \(g(x)=0\text{,}\) we see that \(0\) is our output, so we look for where \(y=0\text{.}\) Looking left and right, we find two points: \((-2,0)\) and \((4,0)\text{.}\) Therefore, we have two answers: \(x=-2,4\text{.}\)
To solve \(g(x)=5\text{,}\) we see that \(5\) is our output, so we look where \(y=5\text{.}\) Looking left and right, we only find one point: \((9,5)\text{,}\) so we have one answer: \(x=9\)
To solve \(g(x)=-7\text{,}\) we see that \(-7\) is our output, so we look for where \(y=-7\text{.}\) Looking left and right, we find no points on the graph! Therefore, our answer is just "none".
When we are given the function as a table, we just remember which column is the output column and which is the input column. If we are given the output, we just look for that number in the output column, rather than in the input column.
Example 2.31.
Suppose \(T(x)\) is given in the table below:
| \(x\) | \(T(x)\) |
| \(-1\) | \(7\) |
| \(0\) | \(0\) |
| \(2\) | \(0\) |
| \(3\) | \(2\) |
| \(7\) | \(0\) |
We want to solve \(T(x)=7\text{.}\) Since \(7\) is our output, we look for \(7\) in the output column, which is the second column (labeled with the \(T(x)\)). We find the \(7\) in the first row of numbers. So, to find our answer, we look in the input column (the first column, labeled with a \(x\)) in the first row of numbers. Therefore, our answer is \(x=-1\text{.}\)
Checkpoint 2.33.
Suppose \(T(x)\) is given in the table below:
| \(x\) | \(T(x)\) |
| \(-1\) | \(7\) |
| \(0\) | \(0\) |
| \(2\) | \(0\) |
| \(3\) | \(2\) |
| \(7\) | \(0\) |
Solve each of the following:
\(\displaystyle T(x)=2\)
\(\displaystyle T(x)=3\)
\(\displaystyle T(x)=0\)
\(\displaystyle x=3\)
none
\(\displaystyle x=0,2,7\)
Solve each of the following:
To solve \(T(x)=2\text{,}\) we see that \(2\) is our output. So, we look for \(2\) in the output column, which is the second column (labeled with the \(T(x)\)). We find the \(2\) in the fourth row of numbers. So, to find our answer, we look in the input column (the first column, labeled with a \(x\)) in the fourth row of numbers. Therefore, our answer is \(x=3\text{.}\)
To solve \(T(x)=3\text{,}\) we see that \(3\) is our output. So, we look for \(3\) in the output column, which is the second column (labeled with the \(T(x)\)). We find that there is no \(3\) in the output column. Therefore, there is no input that leads to \(3\) as the output, so our answer is "none".
To solve \(T(x)=0\text{,}\) we see that \(0\) is our output. So, we look for \(0\) in the output column, which is the second column (labeled with the \(T(x)\)). We find the \(0\) in the second, third, and last rows of numbers. So, to find our answer, we look in the input column (the first column, labeled with a \(x\)) in the second, third, and last rows of numbers. Therefore, our answer is \(x=0, 2, 7\text{.}\)