Section 5.3 Vertical Scales
Example 5.29. Warm-up.
Suppose \(f(x)\) is given in the table below:
| \(x\) | \(f(x)\) |
| \(-1\) | \(2\) |
| \(0\) | \(3\) |
| \(1.3\) | \(-4\) |
| \(7\) | \(0\) |
| \(14\) | \(1\) |
Now, let's define a new function \(g(x)=3f(x)\text{.}\) We want to construct the table for \(g(x)\text{:}\)
| \(x\) | \(g(x)\) |
| \(-1\) | |
| \(0\) | |
| \(1.3\) | |
| \(7\) | |
| \(14\) |
To fill in the top row, we need to find \(g(-1)\text{.}\) Based on our definition of \(g(x)\text{,}\) we have that \(g(-1)=3f(-1)\text{.}\) From the table for \(f(x)\text{,}\) we know that \(f(-1)=2\text{.}\) Therefore,
We can fill out the rest of the table following the same logic:
| \(x\) | \(g(x)\) |
| \(-1\) | \(6\) |
| \(0\) | \(9\) |
| \(1.3\) | \(-12\) |
| \(7\) | \(0\) |
| \(14\) | \(3\) |
Let's compare the two functions we looked at in the warm-up example:
| \(x\) | \(f(x)\) | \(3f(x)\) |
| \(-1\) | \(2\) | \(6\) |
| \(0\) | \(3\) | \(9\) |
| \(1.3\) | \(-4\) | \(-12\) |
| \(7\) | \(0\) | \(0\) |
| \(14\) | \(1\) | \(3\) |
In \(3f(x)\text{,}\) we've multiplied \(3\) by the outside of the function, so all of the outputs are multiplied by \(3\text{.}\) Remember that on a graph, the outputs are represented by the \(y\)-values, so this would multiply all of the \(y\)-values by \(3\text{.}\) So, the graph of \(3f(x)\) would be the same as the graph of \(f(x)\text{,}\) but streteched up and down (away from the \(x\)-axis) by \(3\text{.}\)
Definition 5.34. Vertical Scales.
The graph of \(bf(x)\) is the same as the graph of \(f(x)\text{,}\) but:
if \(b \gt 1\text{,}\) the graph is stretched away from the \(x\)-axis.
if \(0 \lt b \lt 1\text{,}\) the graph is squished/compressed towards the \(x\)-axis.
We call this a vertical scale, since "vertical" means "up/down".
If you look closely at the definition above, you'll see that we are only looking at positive values of \(b\text{.}\) We'll look at what happens when we multiply by a negative number in Section Section 5.5.
See below for an animation of what this transformation does to a graph. If you want to see the animation in a larger window, click here 11 .
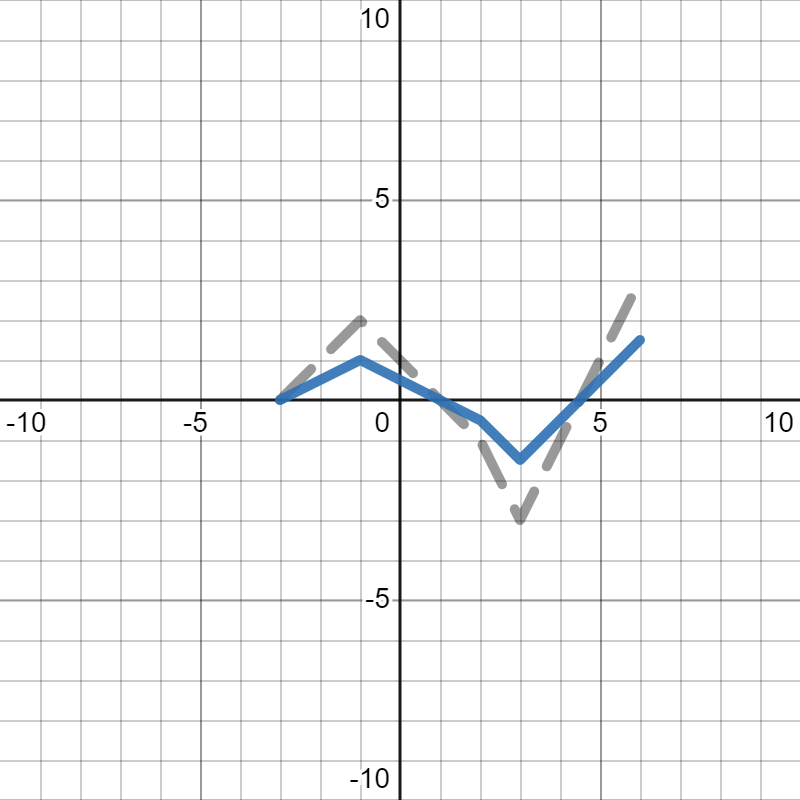
Example 5.35.
Below is the graph of \(h(x)\text{:}\)
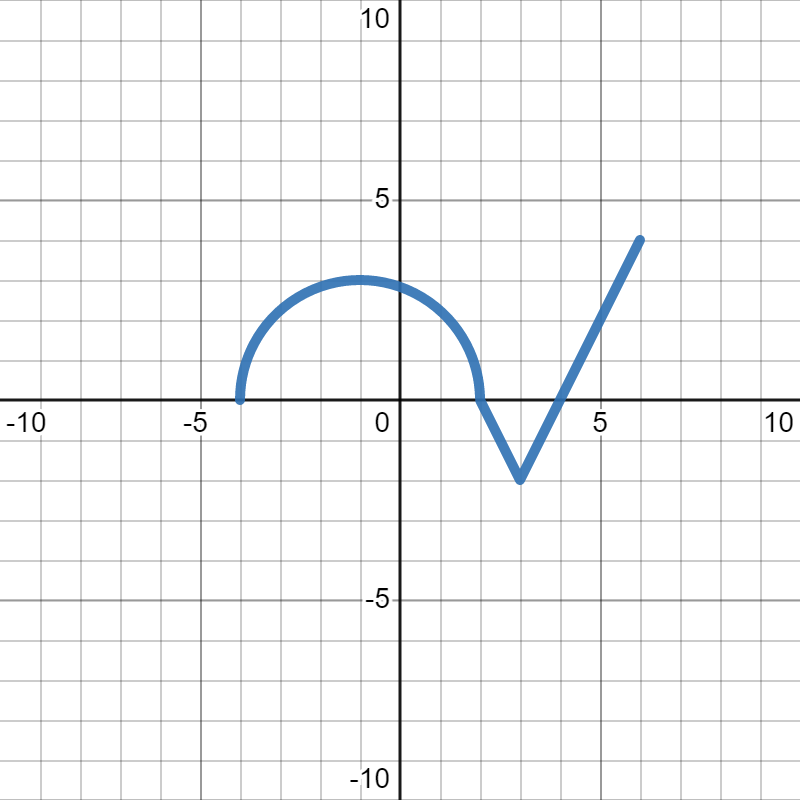
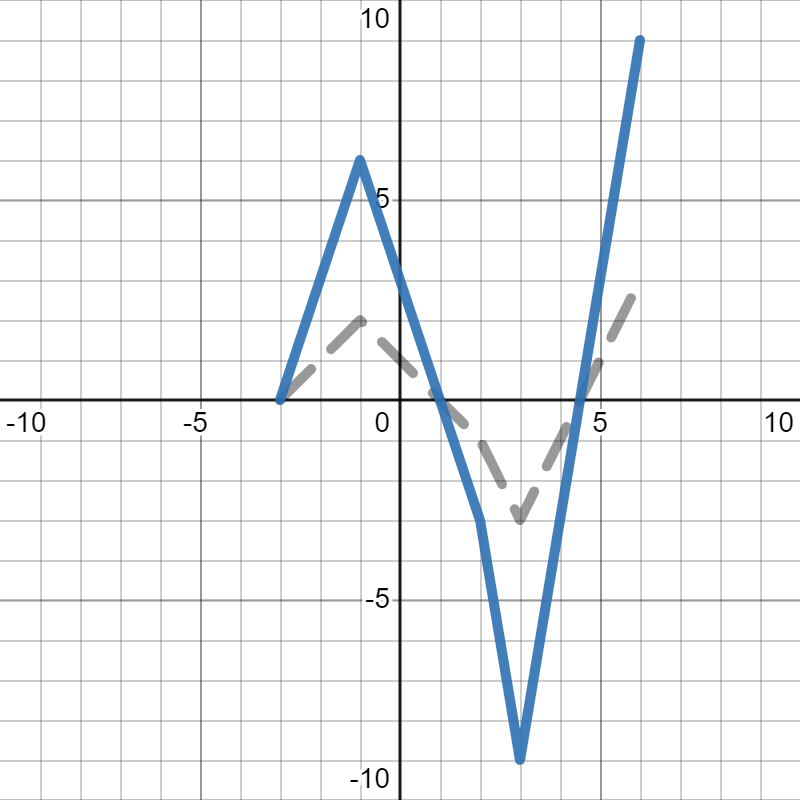
We want to figure out which of the following is the graph of \(2h(x)\text{.}\) In each, the gray dotted graph is the orignal graph of \(h(x)\) so you can more easily see how it changed.
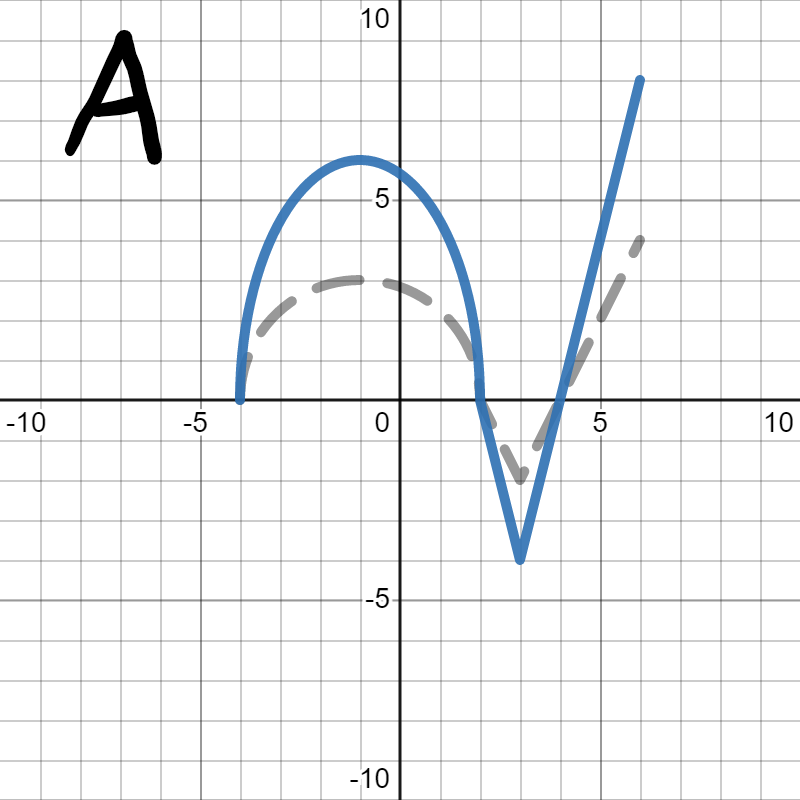
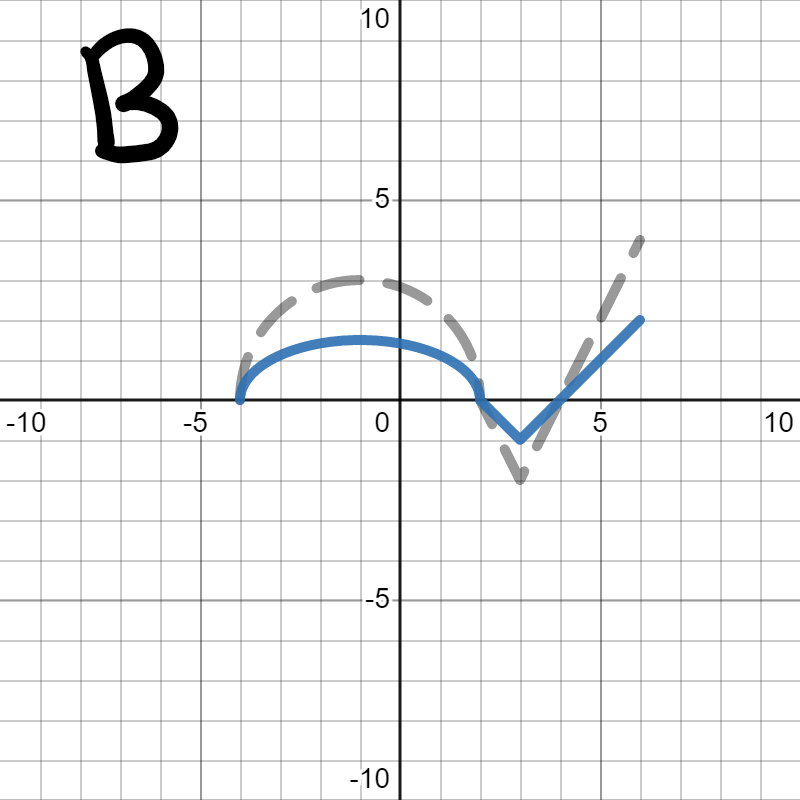
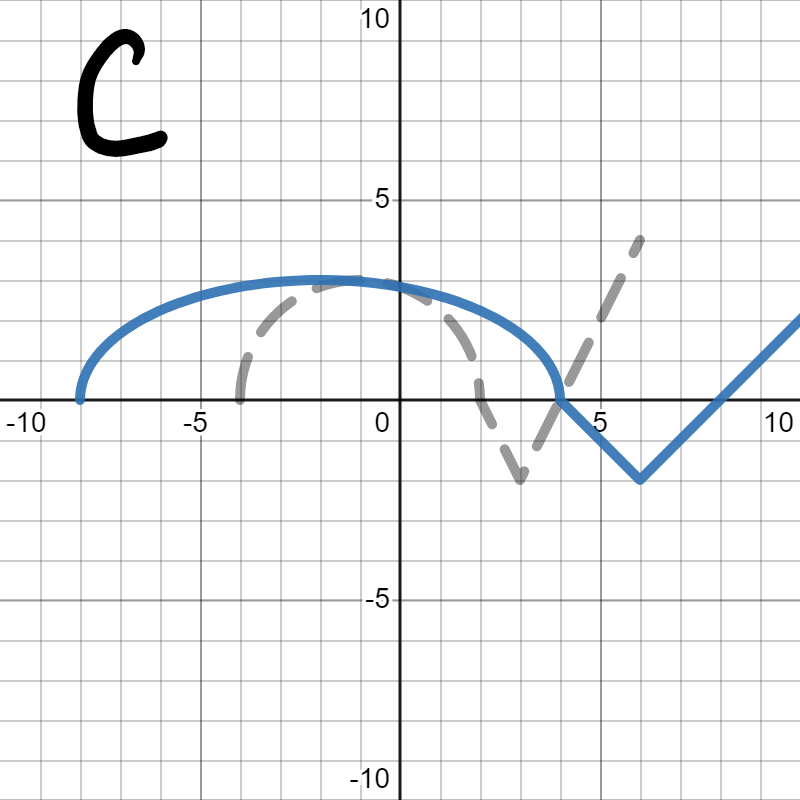
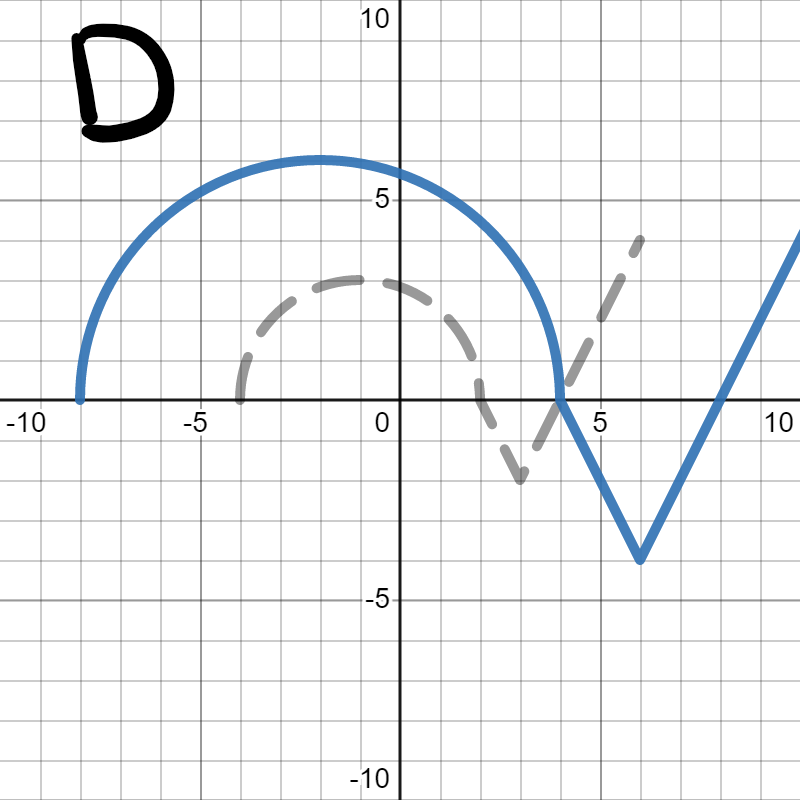
Since we are looking for \(2h(x)\text{,}\) we are looking for the graph to stretch up and down (away from the \(x\)-axis) by 2, which is graph A. Graph B squished towards the \(x\)-axis, which would be \(\frac{1}{2}h(x)\text{.}\) Graph C stretched horizontally instead of vertically, which you'll learn about in Section 5.4. Graph D made the graph twice as big in both directions. We only wanted it to get bigger vertically, not horizontally.
Checkpoint 5.36.
The graph of \(p(x)\) is below:
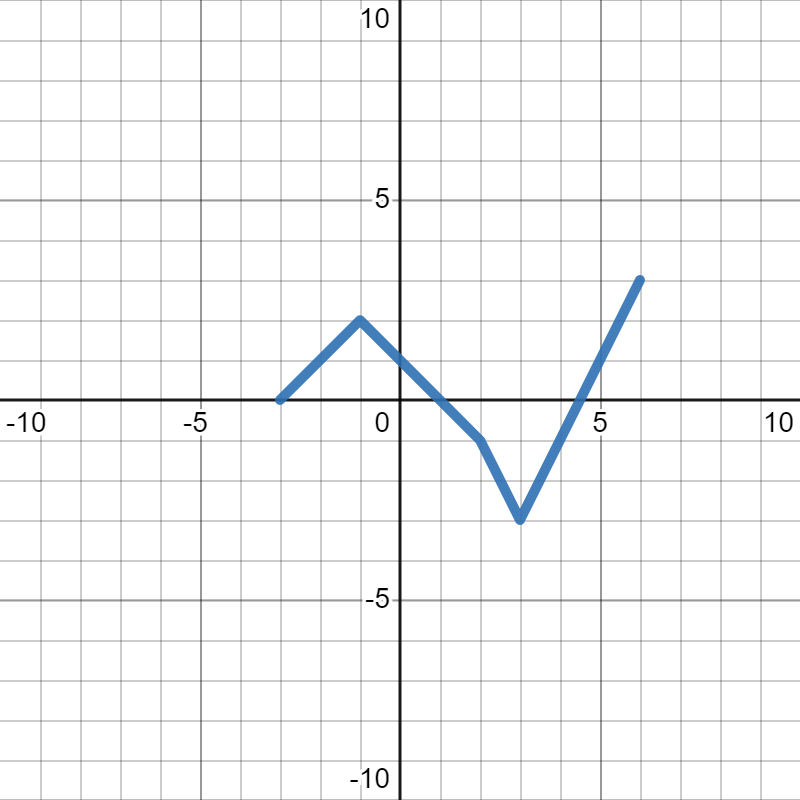
Sketch the graph of each of the following:
\(\displaystyle \frac{1}{2}p(x)\)
\(\displaystyle 3p(x)\)
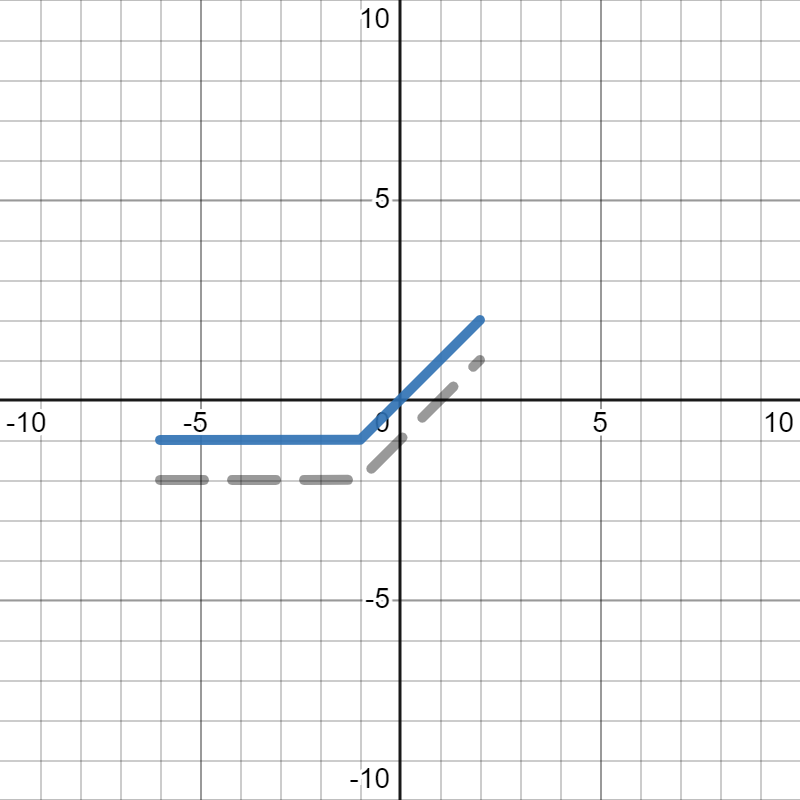
- To draw \(\frac{1}{2}p(x)\text{,}\) we see that we squishing the whole graph vertically in half (towards the \(x\)-axis). Since we are dividing all the \(y\)-values by 2, and \(0\) times anything is still \(0\text{,}\) all of the points on the \(x\)-axis (where \(y=0\)) stay where they are at. Next, we will move the corner points, then connect them together to get the whole graph. So, you would move the point \((-1,2)\) on the original graph down to \((-1,1)\text{.}\) Similarly, you would move the point \((2,-1)\) on the original graph up to \((2,-\frac{1}{2})\text{,}\) move the point \((3,-3)\) on the original graph up to \((3,-1.5)\text{,}\) and move the point \((6,3)\) on the original graph down to \((6,1.5)\text{.}\) From there, you can connect the lines to get the final graph, shown in blue below, where the gray dotted line is the orignal graph of \(p(x)\text{.}\)
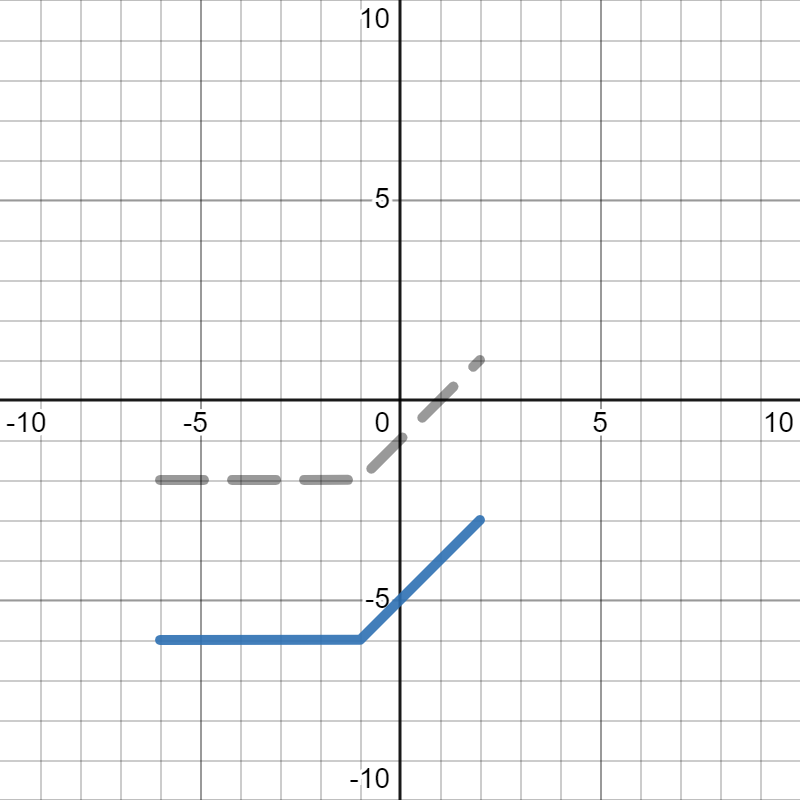
- To draw \(3p(x)\text{,}\) we see that we stretching the whole graph vertically by 3 (away from the \(x\)-axis). Since we are multiplying all the \(y\)-values by 3, and \(0\) times anything is still \(0\text{,}\) all of the points on the \(x\)-axis (where \(y=0\)) stay where they are at. Next, we will move the corner points, then connect them together to get the whole graph. So, you would move the point \((-1,2)\) on the original graph up to \((-1,6)\text{.}\) Similarly, you would move the point \((2,-1)\) on the original graph down to \((2,-3)\text{,}\) move the point \((3,-3)\) on the original graph down to \((3,-9)\text{,}\) and move the point \((6,3)\) on the original graph up to \((6,9)\text{.}\) From there, you can connect the lines to get the final graph, shown in blue below, where the gray dotted line is the orignal graph of \(p(x)\text{.}\)
Example 5.37.
Suppose the solid blue graph below is the graph of \(f(x)\) and the dotted red graph is the graph of \(g(x)\text{:}\)
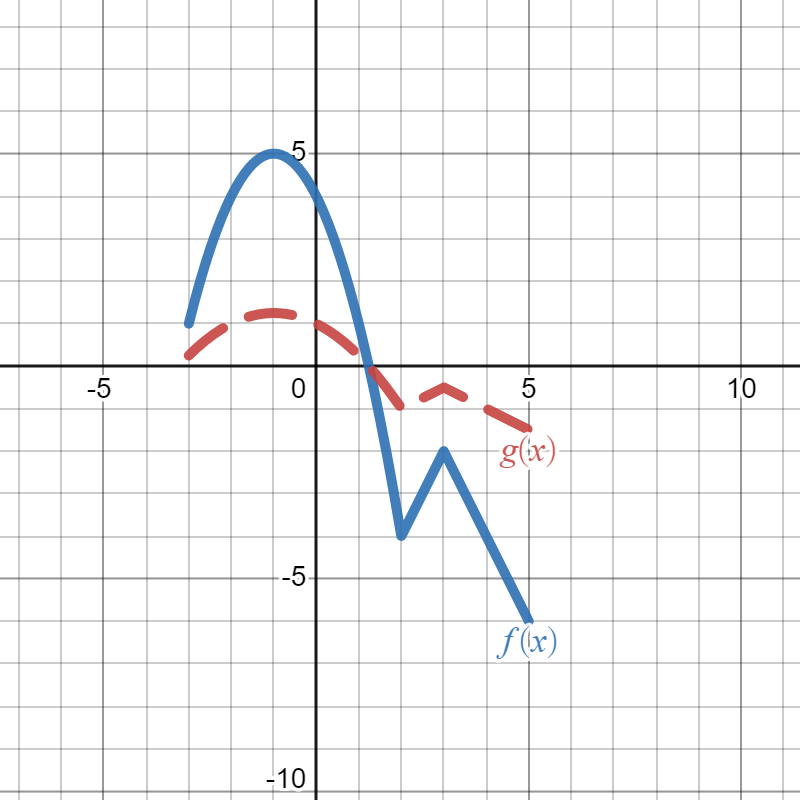
We want to write a formula for \(g(x)\) in terms of \(f(x)\text{.}\) In other words, we start with \(f(x)\) and figure out how the graph changed to get to \(g(x)\text{,}\) then write how that changes the formula. Since the question asks for the formula "in terms of \(f(x)\)", that means we will write \(f(x)\) somewhere in our answer. Looking at the graph, we see that \(g(x)\) is the graph of \(f(x)\) squished vertically (towards the \(x\)-axis) by \(4\text{.}\) Therefore, that means we are dividing by \(4\) on the outside of the function \(f(x)\text{.}\) So, our final answer is \(g(x)=\frac{1}{4}f(x)\text{.}\)
Checkpoint 5.38.
Suppose the solid blue graph below is the graph of \(f(x)\) and the dotted red graph is the graph of \(g(x)\text{:}\)
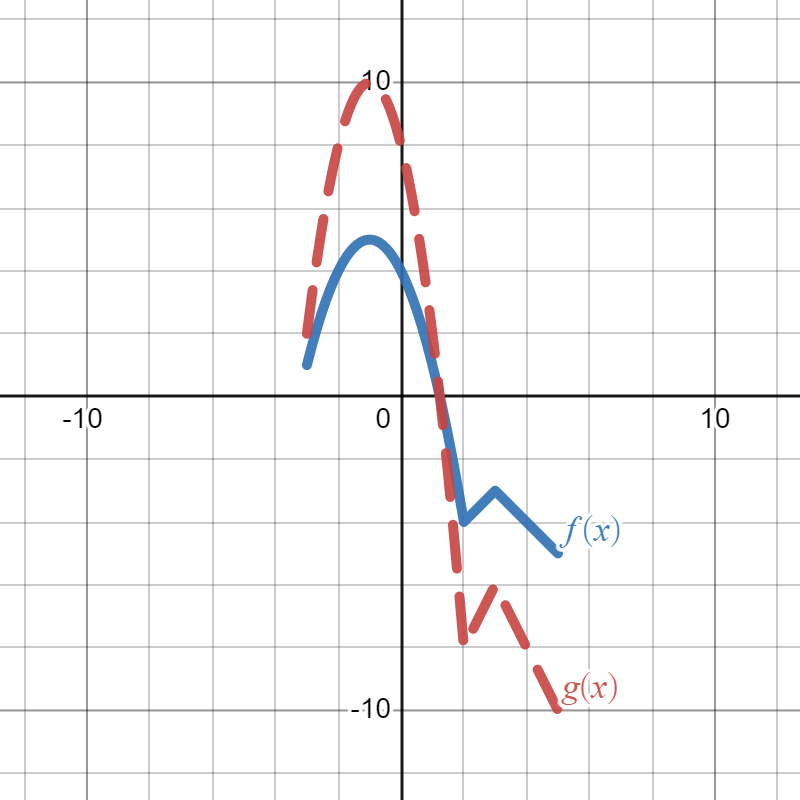
Write a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
\(g(x)=2f(x)\)
We want to write a formula for \(g(x)\) in terms of \(f(x)\text{.}\) In other words, we start with \(f(x)\) and figure out how the graph changed to get to \(g(x)\text{,}\) then write how that changes the formula. Since the question asks for the formula "in terms of \(f(x)\)", that means we will write \(f(x)\) somewhere in our answer. Looking at the graph, we see that \(g(x)\) is the graph of \(f(x)\) stretched vertically (away from the \(x\)-axis) by \(2\text{.}\) Therefore, that means we are multiplying by \(2\) on the outside of the function \(f(x)\text{.}\) So, our final answer is \(g(x)=2f(x)\text{.}\)
Example 5.39.
Suppose \(f(x)=x^2+3x-4\) and \(g(x)\) is the same as \(f(x)\) but stretched vertically by \(7\text{.}\) Let's write a formula for \(g(x)\text{.}\) Since we have an explicit formula for \(f(x)\) in this case, we can write an explicit formula for \(g(x)\text{,}\) too. Since we are stretching vertically by \(7\text{,}\) that means we are multiplying \(7\) to the outside of the function. So,
So our final answer is \(g(x)=7x^2+21x-28\text{.}\)
Checkpoint 5.40.
Suppose \(f(x)=3x^3-2x+1\) and \(g(x)\) is the same as \(f(x)\) but squished vertically by \(4\text{.}\) Write a formula for \(g(x)\text{.}\)
\(g(x)=\frac{3x^3-2x+1}{4}\)
Since we have an explicit formula for \(f(x)\) in this case, we can write an explicit formula for \(g(x)\text{,}\) too. Since we are squishing vertically by \(4\text{,}\) that means we are dividing by \(4\) on the outside of the function. So,
So our final answer is \(g(x)=\frac{3x^3-2x+1}{4}\text{.}\)
Example 5.41.
Suppose \(f(x)=x^2-x+5\) and \(g(x)=3x^2-3x+15\text{.}\) Let's figure out what transformations took \(f(x)\) to \(g(x)\text{.}\) Comparing the two formulas, we see that in the formula for \(g(x)\text{,}\) all of the numbers are multiplied by \(3\text{.}\) That means that to get from \(f(x)\) to \(g(x)\text{,}\) we must have multiplied by \(3\) on the outside so that \(g(x)=3f(x)\text{.}\) That means there was a vertical stretch by \(3\text{.}\)
Checkpoint 5.42.
Suppose \(f(x)=3x+2\) and \(g(x)=\frac{3}{5}x+\frac{2}{5}\text{.}\) What transformations took \(f(x)\) to \(g(x)\text{?}\)
Vertical squish/compression by \(5\text{.}\)
Comparing the two formulas, we see that in the formula for \(g(x)\text{,}\) all of the numbers are divided by \(5\text{.}\) That means that to get from \(f(x)\) to \(g(x)\text{,}\) we must have divided by \(5\) on the outside so that \(g(x)=\frac{f(x)}{5}\text{.}\) That means there was a vertical squish by \(5\text{.}\)
https://www.desmos.com/calculator/h2jzfauy6c